Xét hai tam giác vuông \(AEI\) và \(ADI\) có:
\(AI\) chung
\(AE=AD\) (gt)
\(\widehat {AEI} = \widehat {ADI} = {90^o}\)
\( \Rightarrow ΔAEI = ΔADI\) (cạnh huyền - cạnh góc vuông).
\( \Rightarrow EI=DI\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(BEI\) và \(CDI\) có:
\(\widehat {BEI} = \widehat {CDI} = {90^o}\)
\(EI=DI\) (chứng minh trên)
\(BE=CD\) (gt)
\( \Rightarrow ΔBEI = ΔCDI\) (c.g.c)
\( \Rightarrow BI =CI\) (hai cạnh tương ứng).
\(AE=AD\) (gt)
\(BE=CD\) (gt)
\( \Rightarrow AE+BE=AD+CD\)
\( \Rightarrow AB=AC\).
Xét \(ΔAIB \) và \( ΔAIC\) có:
\(AB=AC\) (chứng minh trên)
\(BI=CI\) (chứng minh trên)
\(AI\) cạnh chung
\( \Rightarrow ΔAIB = ΔAIC\) (c.c.c)
Xét \(ΔABD\) và \(ΔACE\) có:
\(AB=AC\) (chứng minh trên)
\(AD=AE\) (gt)
\(\widehat A\) chung
\( \Rightarrow ΔABD = ΔACE\) (c.g.c)
\( \Rightarrow BD=CE\) (hai cạnh tương ứng).
Xét \(ΔBEC\) và \(ΔCDB\) có:
\(CE=BD\) (chứng minh trên)
\(BC \) chung
\(BE = CD\) (gt)
\( \Rightarrow ΔBEC = ΔCDB\) (c.c.c).
Vậy có \(5\) cặp tam giác bằng nhau.
Chọn D.
Bài II.2
Cho hình bs 7. Chứng minh rằng \(OA = OB\).
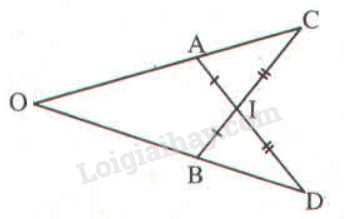
Phương pháp:
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
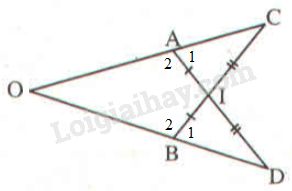
Xét \(ΔAIC\) và \(ΔBID\) có:
\(IA=IB\) (gt)
\(IC=ID\) (gt)
\(\widehat {AIC} = \widehat {BID}\) (đối đỉnh)
\( \Rightarrow ΔAIC = ΔBID\) (c.g.c)
\(\Rightarrow \widehat C = \widehat D\) (hai góc tương ứng)
\( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) (hai góc tương ứng) (1)
\(\widehat {{A_1}} + \widehat {{A_2}} = {180^o}\) (hai góc kề bù) (2)
\(\widehat {{B_1}} + \widehat {{B_2}} = {180^o}\) (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra \(\widehat {{A_2}} = \widehat {{B_2}}\)
\(IA=IB\) (gt)
\(IC=ID\) (gt)
\(\begin{array}{l} \Rightarrow IA + ID = IB + IC\\ \Rightarrow AD = BC\end{array}\)
Xét \(ΔOAD \) và \( ΔOBC\) có:
\(AD=BC\) (chứng minh trên)
\(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh trên)
\( \widehat C = \widehat D\) (chứng minh trên)
\( \Rightarrow ΔOAD = ΔOBC \) (g.c.g).
\( \Rightarrow OA = OB\) (hai cạnh tương ứng).
Bài II.3
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BA\) lấy điểm \(D\), trên tia đối của tia \(CA\) lấy điểm \(E\) sao cho \(BD = CE.\) Gọi \(I\) là giao điểm của \(BE\) và \(CD\).
a) Chứng minh rằng \(IB = IC, ID = IE.\)
b) Chứng minh rằng \(BC\) song song \(DE.\)
c) Gọi \(M\) là trung điểm \(BC.\) Chứng minh rằng ba điểm \(A, M, I\) thẳng hàng.
Phương pháp:
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Qua một điểm ta kẻ được duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
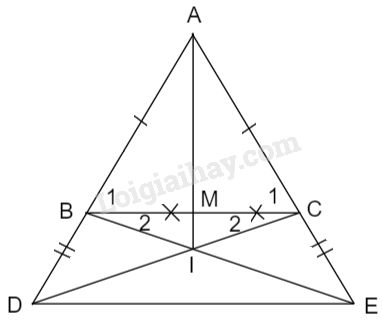
a) \(AB=AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(BD=CE\) (gt)
\( \Rightarrow AB+BD=AC+CE\)
\( \Rightarrow AD=AE\)
Xét \(ΔABE\) và \(ΔACD\) có:
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat A\) chung
\(AE = AD\)
\(⇒ ΔABE = ΔACD\) (c.g.c)
\(⇒ BE = CD\) (hai cạnh tương ứng) (1)
\( \Rightarrow \widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng) (2)
Tam giác \(ABC\) cân tại \(A\) nên \(\widehat {{B_1}} = \widehat {{C_1}}\) (3)
Từ (2) và (3) suy ra \(\widehat {ABE} - \widehat {{B_1}} = \widehat {ACD} - \widehat {{C_1}} \)
\(\Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\)
\(⇒ ΔBIC\) cân tại \(I\)
\(⇒ IB = IC\) (tính chất tam giác cân) (4)
Từ (1) và (4) suy ra \(BE - IB = CD - IC\), tức là \(IE = ID.\)
b) \(\Delta ABC\) cân tại \(A\) nên \(\widehat {{B_1}} = \dfrac{{{{180}^o} - \widehat A}}{2}\) (5)
\(\Delta ADE\) cân tại \(A\) nên \(\widehat {ADE} = \dfrac{{{{180}^o} - \widehat A}}{2}\) (6)
Từ (5) và (6) suy ra \(\widehat {{B_1}} = \widehat {ADE}\)
Mà \(\widehat {{B_1}} \) và \( \widehat {ADE}\) ở vị trí đồng vị nên \(BC // DE.\)
c) Xét \(ΔABM\) và \(ΔACM\) có:
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {{B_1}} = \widehat {{C_1}}\) (vì \(\Delta ABC\) cân tại \(A\))
\(BM = CM\) (vì \(M\) là trung điểm của \(BC\))
\(⇒ ΔABM = ΔACM\) (c.g.c)
\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng)
Mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^o}\) hay \(AM ⊥ BC\).
Xét \(\Delta BMI \) và \(\Delta CMI\) có:
\(IB=IC\) (chứng minh trên)
\(\widehat {{B_2}} = \widehat {{C_2}}\) (chứng minh trên)
\(BM = CM\) (vì \(M\) là trung điểm của \(BC\))
\( \Rightarrow \Delta BMI = \Delta CMI\) (c.g.c)
\( \Rightarrow \widehat {BMI} = \widehat {CMI}\) (hai góc tương ứng)
Mà \(\widehat {BMI} + \widehat {CMI} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {BMI} = \widehat {CMI} = {90^o}\) hay \(IM ⊥ BC\)
\(⇒ A, I, M\) thẳng hàng (qua một điểm ta kẻ được duy nhất một đường thẳng vuông góc với đường thẳng cho trước).