\(\displaystyle {\rm{A}} = {{1.3} \over {2.2}}.{{2.4} \over {3.3}}.{{3.5} \over {4.4}}...{{29.31} \over {30.30}}\)
\(\displaystyle A= {{1.2.3...29} \over {2.3.4...30}}.{{3.4.5...31} \over {2.3.4...30}}\)
\(\displaystyle A = {1 \over {30}}.{{31} \over 2} = {{31} \over {60}}\)
Bài 11.6*
Chứng tỏ rằng \(\displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + ... + {1 \over {17}} < 2\)
\(\displaystyle {1 \over 5} + {1 \over 6} + {1 \over 7} + {1 \over 8} + {1 \over 9} < {1 \over 5}.5 = 1\) \((1)\)
\(\displaystyle {1 \over {10}} + {1 \over {11}} + ... + {1 \over {16}} + {1 \over {17}} < {1 \over 8}.8 = 1\) \((2)\)
Cộng theo từng vế \((1)\) và \((2)\) ta được:
\(\displaystyle {1 \over 5} + {1 \over 6} + ... + {1 \over {17}} < 2.\)
Bài 11.7*
Tính giá trị của biểu thức :
\(\displaystyle M = {1 \over {1.2.3}} + {1 \over {2.3.4}} + {1 \over {3.4.5}} + ... \)\(\displaystyle + {1 \over {10.11.12}}\)
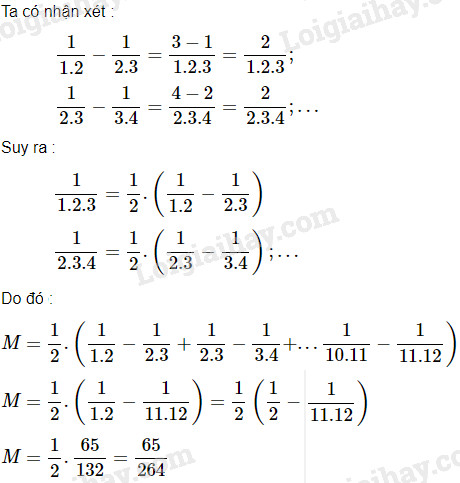
Phương pháp giải Phân tích tử số và mẫu số thành tích của các thừa số, sau đó cùng chia cả tử và mẫu cho các thừa số chung.
- So sánh các phân số \(\displaystyle {1 \over 5} ; {1 \over 6} \; {1 \over 7};{1 \over 8} \; {1 \over 9}\) với phân số \(\displaystyle {1 \over 5}.\)
- So sánh các phân số \(\displaystyle {1 \over 10} ; {1 \over 11} \;... \; ;{1 \over 17}\) với phân số \(\displaystyle {1 \over 8}.\)
Ta có nhận xét ;
\(\displaystyle {1 \over {1.2}} - {1 \over {2.3}} = {{3 - 1} \over {1.2.3}} = {2 \over {1.2.3}};\)
\(\displaystyle {1 \over {2.3}} - {1 \over {3.4}} = {{4 - 2} \over {2.3.4}} = {2 \over {2.3.4}};...\)
Suy ra:
\(\displaystyle {1 \over {1.2.3}} = {1 \over 2}.\left( {{1 \over {1.2}} - {1 \over {2.3}}} \right)\)
\(\displaystyle {1 \over {2.3.4}} = {1 \over 2}.\left( {{1 \over {2.3}} - {1 \over {3.4}}} \right);...\)
Ta tiếp tục là tương tự với các phân số còn lại, từ đó tính được tổng \(M.\)