a) Ta có: \(3\overrightarrow {OC} - \overrightarrow {OB} \)\( = 3(\overrightarrow {OM} + \overrightarrow {MC} ) - (\overrightarrow {OM} + \overrightarrow {MB} )\)
\( = 3(\overrightarrow {OM} - \overrightarrow {OM} ) + (3\overrightarrow {MC} - \overrightarrow {MB} )\)\( = 2\overrightarrow {OM} \)
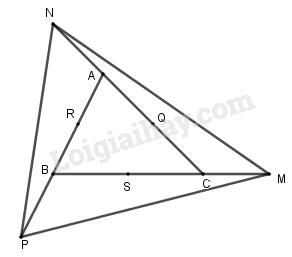
b) Gọi \(S, Q\) và \(R\) lần lượt là trung điểm của \(BC, CA\) và \(AB\).
\(\overrightarrow {MB} = 3\overrightarrow {MC} \Rightarrow \overrightarrow {CM} = \overrightarrow {SC} \); \(\overrightarrow {NC} = 3\overrightarrow {NA} \Rightarrow \overrightarrow {AN} = \overrightarrow {CQ} \)
\(\overrightarrow {PA} = 3\overrightarrow {PB} \Rightarrow \overrightarrow {BP} = \overrightarrow {RB} = \overrightarrow {QS} \)
Gọi \(G\) là trọng tâm của tam giác \(ABC\) thì \(\overrightarrow {GA} + \overrightarrow {BG} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có:
\(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GP} \)\( = \overrightarrow {GC} + \overrightarrow {CM} + \overrightarrow {GA} + \overrightarrow {AN} + \overrightarrow {GB} + \overrightarrow {BP} \)
\( = \left( {\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {SC} + \overrightarrow {CQ} + \overrightarrow {QS} } \right)\)\( = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)
Vậy \(G\) là trọng tâm của tam giác \(MNP\).