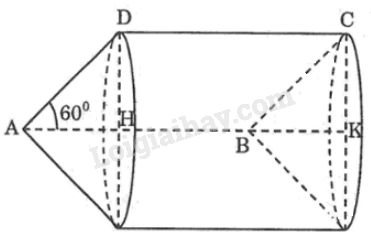
a) Khi quay hình bình hành \(ABCD\) một vòng quanh cạnh \(AB\) thì cạnh \(AD\) và \(BC\) vạch nên \(2\) hình nón bằng nhau có đường sinh \(AD = BC = x,\) cạnh \(CD\) vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Trong \(∆AHD\) có \(\widehat {AHD} = 90^\circ ;\widehat A = 60^\circ \), ta có:
\(DH = AD. \sin 60^o= \displaystyle x.{{\sqrt 3 } \over 2} = {{x\sqrt 3 } \over 2}\)
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh \(2\) hình nón và diện tích xung quanh hình trụ: \(S = {S _{\text{xq trụ}}} + 2{S _\text{xq nón}}\)
\(\eqalign{
& S = 2\pi DH.DC + 2.\pi DH.AD \cr
& \;\;\;= 2\pi {{x\sqrt 3 } \over 2}.1 + 2.\pi .{{x\sqrt 3 } \over 2}.x \cr
& \;\;\;= \pi x\sqrt 3 + \pi {x^2}\sqrt 3 \cr} \)
\( \Rightarrow S = \pi x\sqrt 3 (1 + x)\)
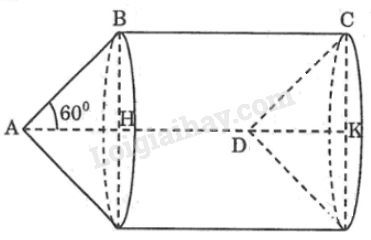
Khi quay hình bình hành quanh trục \(AD\) một vòng thì cạnh \(AB\) và \(DC\) vạch nên hai hình nón bằng nhau có đường sinh \(AB = CD = 1.\) Cạnh \(BC\) vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Bán kính đáy: \(\displaystyle BH = AB. \sin 60^o = 1.{{\sqrt 3 } \over 2}={{\sqrt 3 } \over 2}\)
\(S_1\) là diện tích toàn phần hình tạo thành bằng tổng diện tích xung quanh hai hình nón cộng với diện tích hình trụ.
\(S_1 = {S _{\text{xq trụ}}} + 2{S _\text{xq nón}}\)
\({S_1} = 2\pi .BH.BC + 2.\pi .BH.AB\)
\(S_1\displaystyle = 2\pi. {{\sqrt 3 } \over 2}.x + 2.\pi .{{\sqrt 3 } \over 2}.1\)
\({S_1} = \pi \sqrt 3 (x + 1)\)
b) Để \(S = S_1\) \(\Leftrightarrow \pi x\sqrt 3 (1 + x) = \pi \sqrt 3 (x + 1) \)
\(\Leftrightarrow x(1 + x) = x + 1\)
\( \Leftrightarrow x\left( {x + 1} \right) - \left( {x + 1} \right) = 0\)
\( \Leftrightarrow (x + 1)(x - 1) = 0\)
Vì \(x > 0 \Rightarrow x + 1 \ne 0\)
\( \Rightarrow x - 1 = 0 \Leftrightarrow x = 1\)
Vậy \(x=1\) thì \(S = S_1\).
Để \(S = 2S_1\) \(\Leftrightarrow \pi x\sqrt 3 (1 + x) = 2\pi \sqrt 3 (x + 1) \)
\(\Leftrightarrow x(x + 1) = 2(x + 1)\)
\( \Leftrightarrow x\left( {x + 1} \right) - 2\left( {x + 1} \right) = 0\)
\( \Leftrightarrow (x + 1)(x - 2) = 0\)
Vì \(x > 0 \Rightarrow x + 1 \ne 0\)
\( \Rightarrow x - 2 = 0 \Leftrightarrow x = 2\).
Vậy \(x=2\) thì \(S = 2S_1\).