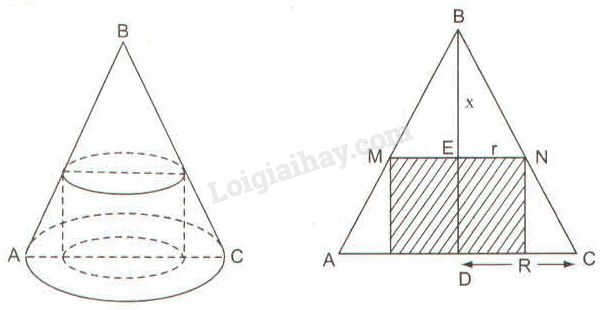
Gọi bán kính đáy hình nón là \(R\), chiều cao hình nón là \(h\), bán kính đáy hình trụ là \(r\), chiều cao phần hình nón cắt đi là \(BE = x\).
Vì \(MN//AC \), theo hệ quả định lí Ta-lét ta có:
\(\displaystyle {{ME} \over {AD}} = {{BE} \over {BD}}\) hay \(\displaystyle {r \over R} = {x \over h} \Rightarrow r = {{Rx} \over h}\)
Thể tích hình trụ là: \(V = πr^2. (h-x)\)
\(\displaystyle V = \pi .{\left( {{{Rx} \over h}} \right)^2}.\left( {h - x} \right)\)\(\, \displaystyle = \pi .{{{R^2}{x^2}} \over {{h^2}}}.(h - x)\)
Phần bỏ đi của hình nón ít nhất có nghĩa là thể tích của hình trụ lớn nhất:
\(\displaystyle V = \pi .{{{R^2}{x^2}} \over {{h^2}}}(h - x)\)
\(\displaystyle \Rightarrow 2V{h^2} = \pi {R^2}{x^2}(2h - 2x)\)
\(\displaystyle \Rightarrow {{2V{h^2}} \over {\pi {R^2}}} = {x^2}(2h - 2x)\))
Vì \(π, R, h\) là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi \({x^2}\left( {2h - 2x} \right)\) lớn nhất. Ta có \({x^2}\left( {2h - 2x} \right) = x.x.\left( {2h - 2x} \right)\)
Áp dụng bất đẳng thức Cô - si cho ba số dương \(x, x, 2h-2x\) ta có:
\(\sqrt[3]{{x.x.\left( {2h - 2x} \right)}} \le \dfrac{{x + x + 2h - 2x}}{3} = \dfrac{{2h}}{3}\) \( \Rightarrow x.x.\left( {2h - 2x} \right) \le {\left( {\dfrac{{2h}}{3}} \right)^3} \) \(= \dfrac{{8{h^3}}}{{27}}\)
Dấu "=" xảy ra khi \( x = 2h -2x \Leftrightarrow 3x = 2h \) \(\Rightarrow x = \displaystyle {2 \over 3}h\)
Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng \(\displaystyle {2 \over 3}\) chiều cao hình nón thì phần bỏ đi là ít nhất.