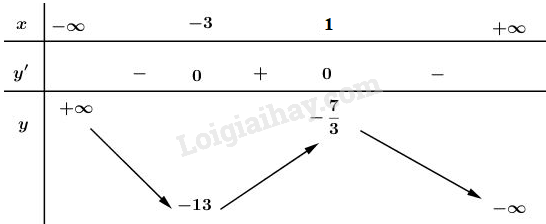
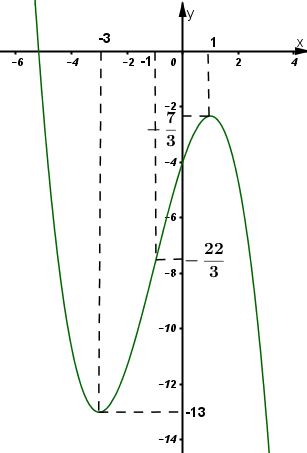
Bài 2 trang 145 SGK Giải tích 12
Lời giải
Bài Tập và lời giải
Đề bài
Cho tam giác \(ABC\). Hãy vẽ một đoạn thẳng \(AD\) sao cho \(AD=BC\) và đường thẳng \(AD\) song song với đường thẳng \(BC.\)
Đề bài
Vẽ hai đường thẳng \(xx', yy'\) sao cho \(xx' // yy'.\)
Đề bài
Cho góc nhọn \(xOy\) và một điểm \(O'\). Hãy vẽ một góc nhọn \(x'Oy'\) có \(O'x' // Ox\) và \(O'y' // Oy.\) Hãy đo xem hai góc \(xOy\) và \(x'O'y'\) có bằng nhau hay không?
Đề bài
Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B (xem hình vẽ).
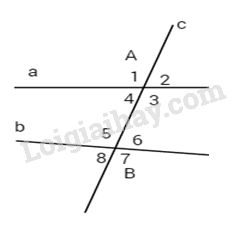
a) Hãy kể tên các cặp góc so le trong, các cặp góc đồng vị, các cặp góc trong cùng phía.
b) Cho \(\widehat {{B_6}} = \widehat {{B_8}} = {80^o}\) \(\widehat {{A_1}} = {120^o}\) và \(\widehat {{B_7}} = {100^o}\). Hãy tính các góc còn lại.
Đề bài
Xem hình vẽ biết \(\widehat {{A_4}} = {50^o}\) và \(\widehat {{B_2}} = {50^o}.\)
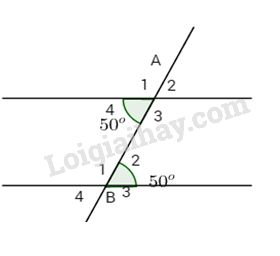
a) Hãy tính các góc còn lại.
b) Hãy so sánh số đo của hai góc so le trong bất kì, hai góc đồng vị bất kì.
c) Tính \(\widehat {{A_3}} + \widehat {{B_2}}\) và \(\widehat {{A_4}} + \widehat {{B_1}}\). Em có kết luận gì về tổng hai góc trong cùng phía?
Đề bài
Cho \(\widehat {xOy} = {40^o}\). Lấy A trên tia Ox. Vẽ tia At nằm trên nửa mặt phẳng bờ là đường thẳng Ox. Chứa tia Oy sao cho At cắt Oy tại B và \(\widehat {OAt} = {100^o}\). Gọi Am là tia phân giác của góc \(\widehat {xAt}\).
a) Chứng tỏ Am // Oy.
b) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng Oy vẽ tia Bn. Hỏi để Bn song song với Ox thì số đo góc OBn phải bằng bao nhiêu?
Đề bài
Cho góc \(\widehat {xOy} = {120^o}\). Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là Ox, vẽ tia At sao cho \(\widehat {OAt} = {60^o}\). Gọ At’ là tia đối của tia At.
a) Chứng tỏ tt’ // Oy.
b) Gọi Om, An theo thứ tự là các tia phân giác của các góc \(\widehat {xOy}\) và \(\widehat {xAt}\). Chứng tỏ Om//An.
Đề bài
Cho hình vẽ bên, biết
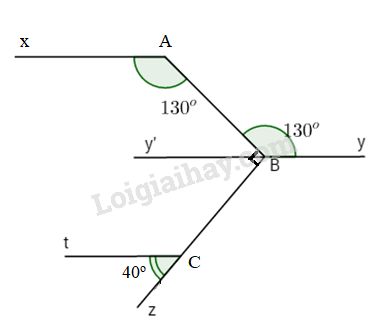
\(\widehat {tCz}\), \(\widehat {xAB} = {130^o},\)
\(\widehat {ABy} = {130^o},\)
\(AB \bot BC,\,\widehat {tCz} = {40^o}.\)
a) Chứng tỏ Ax // By.
b) Chứng tỏ By // Ct.