Bài 12 trang 147 SGK Giải tích 12
Lời giải
Bài Tập và lời giải
Đề bài
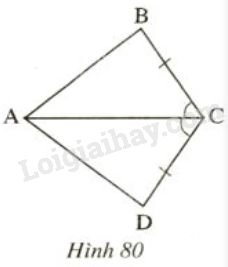
Hai tam giác trên hình 80 có bằng nhau không? Vì sao?
Đề bài
Vẽ tam giác \(ABC\) biết \(\widehat{A}= 90^o;AB=AC=3cm.\) Sau đó đo các góc \(B\) và \(C.\)
Đề bài
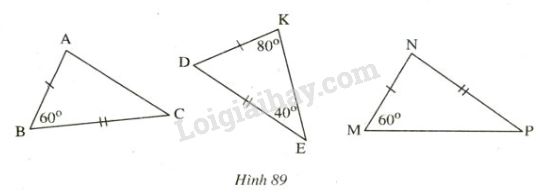
Trên mỗi hình sau có các tam giác nào bằng nhau? Vì sao?
Đề bài
Xét bài toán:
" Cho tam giác \(ABC, M\) là trung điểm của \(BC.\) Trên tia đối của \(MA\) lấy điểm \( E\) sao cho \(ME=MA.\) Chứng minh rẳng \(AB//CE.\)
Dưới đây là hình vẽ và giả thiết, kết luận của bài toán (h.85)
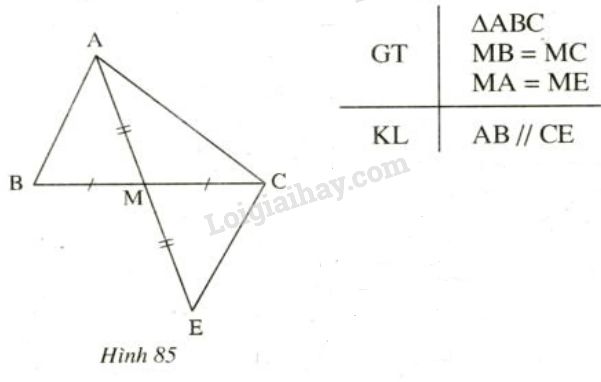
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:
1) \(MB = MC\) (giả thiết)
\(\widehat{AMB}=\widehat{EMC}\) (hai góc đối đỉnh)
\(MA= ME\) (giả thiết)
2) Do đó \(∆AMB=∆EMC\) (c.g.c)
3) \(\widehat{MAB}=\widehat{MEC}\) \( \Rightarrow AB//CE\) (có hai góc bằng nhau ở vị trí so le trong)
4) \(∆AMB= ∆EMC\) \( \Rightarrow \widehat{MAB}=\widehat{MEC}\) (hai góc tương ứng)
5) \(∆AMB\) và \( ∆EMC\) có:
Đề bài
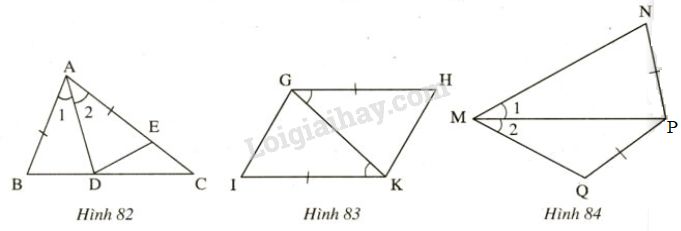
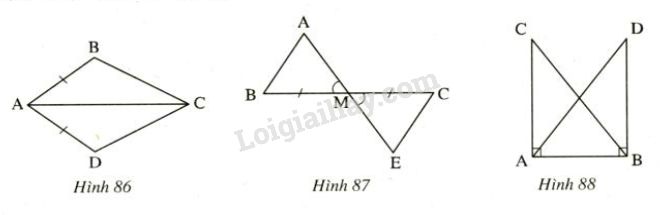
Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh-góc- cạnh.
a) \(∆ABC= ∆ADC\) (h.86);
b) \(∆AMB= ∆EMC\) (H.87)
c) \(∆CAB= ∆DBA\). (h.88)
Đề bài
Cho góc \(xAy\). Lấy điểm \(B\) trên tia \(Ax\), điểm \(D\) trên tia \(Ay\) sao cho \(AB=AD\).Trên tia \(Bx\) lấy điểm \(E\), trên tia \(Dy\) lấy điểm \(C\) sao cho \(BE=DC\). Chứng minh rằng \(\Delta ABC = \Delta ADE\).
Đề bài
Cho đoạn thẳng \(AB\), điểm \(M\) nằm trên đường trung trực của \(AB\). So sánh độ dài các đoạn thẳng \(MA\) và \( MB.\)
Đề bài
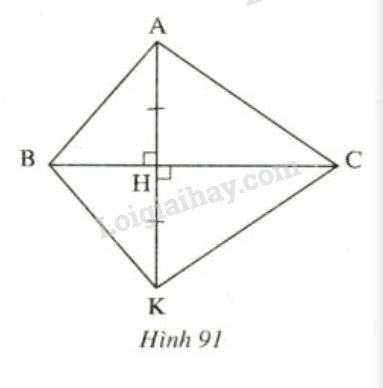
Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.
Đề bài
Cho tam giác ABC có \(AB = AC\), M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.
Đề bài
Cho đoạn thẳng AB, đường trung trực d của AB tại I, trên cùng một nửa mặt phẳng bờ là đường thẳng AB lấy hai điểm C và D thuộc d (D nằm giữa hai điểm C và I). Hãy so sánh hai góc ADI và góc BDI.
Đề bài
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Trên tia đối của tia MC lấy E sao cho ME = MC. Trên tia đối của tia NB lấy F sao cho NF = NB. Chứng minh A là trung điểm của EF.
Đề bài
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng bờ là đường thẳng BC chứa điểm A vẽ tia Cx song song với AB. Trên tia Cx lấy D sao cho \( \Rightarrow \widehat {AMC} + \widehat {CMD} = {180^o}\), \(CD = AB\). Chứng minh:
a)\(MA = MD.\)
b) Ba điểm A, M, D thẳng hàng.
Đề bài
Cho góc \(\widehat {xOy}\). Lấy A, C thuộc tia Ox sao cho OC< OA. Trên tia Oy lấy B và D sao cho \(OB = OA,\,OD = OC.\)
a) Chứng minh AD = BC và
b) Gọi I là giao điểm của AD và BC. Cho biết IA = IB. Chứng minh OI là tia phân giác của góc \(\widehat {xOy}\).
Đề bài
Cho góc bẹt \(\widehat {xOy}\) có phân giác Ot. Trên Ot lấy hai điểm A và B (A nằm giữa O và B). Lấy điểm C thuộc Ox, sao cho OC = OB. Lấy điểm D thuộc Oy sao cho OD = OA. Chứng minh:
a) \(AC= BD\)
b) \(AC \bot BD.\)
Đề bài
Cho tam giác ABC. Trên tia đối của ác tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC.
a)Chứng minh DE // BC.
b) Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh A là trung điểm của MN.
Đề bài
Cho \(\Delta ABC\) có AB = AC, tia phân giác của góc A cắt cạnh BC tại D. Lấy E trên AD. Chứng minh rằng:
a) \(\Delta AEB = \Delta AEC\)
b) ED là tia phân giác của góc \(\widehat {BEC}\)
c) \(AD \bot BC.\)
Đề bài
Cho tam giác ABC có ba góc nhọn, vẽ \(\widehat {EAF} = {120^o} \Rightarrow \widehat {AEF} = \widehat {AFE} = {30^o}. \) \(AH \bot BC\) (H thuộc BC). Từ H vẽ HI, HK lần lượt vuông góc với AB và AC, \(I \in AB,\,K \in AC.\) Trên tia đối của tia IH, KH lần lượt lấy các điểm E, F sao cho \(IE = IH\) và \(KF = KH.\)
a) Chứng minh \(AE = AF.\)
b) Giả sử cho \(\widehat {BAC} = {60^o}\). Hãy tính số đo các góc của .
Đề bài
Cho góc nhọn \(\widehat {xOy}\). Trên Ox lấy hai điểm A và B sao cho OA < OB. Trên Oy lấy hai điểm C và D sao cho OC = OB; OD = OA. Hai đoạn thẳng AC và BD cắt nhau tại E. Chứng minh rằng:
a) AC = BD.
b) \(\Delta EAB = \Delta EDC\)
Đề bài
Cho tam giác ABC (AB < AC). Gọi M trung điểm của BC. Vẽ BH vuông góc với AM (H thuộc AM) và CK vuông góc với AM (K thuộc AM). Chứng minh rằng BH = CK.
Đề bài
Cho tam giác ABC. Trên cạnh BC lấy hai điểm D và E sao cho D nằm giữa B và E và BD = CE. Qua D và E vẽ DF và EH song song với AB. (F và H thuộc AC).
Chứng minh rằng: AB = DF + EH.
Đề bài
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I.
a) Biết \(\widehat A = {70^o}\). Tính số đo góc \(\widehat {BIC}.\)
b) Vẽ \(ID \bot AB\) (D thuộc AB), \(IE \bot BC\) (E thuộc BC), \(IF \bot AC\) (F thuộc AC). Chứng minh rằng: \(ID = IE = IF.\)
Đề bài
Cho góc \(\widehat {xOy}\) khác góc bẹt, có Ot là tia phân giác. Qua điểm H thuộc tia Ot kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự ở A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh B, C, E thẳng hàng.
Đề bài
Cho tam giác ABC có \(\widehat B = \widehat C\). Tia phân giác của góc A cắc BC tại D. Chứng minh:
a) \(\Delta ADB = \Delta ADC\)
b) \(AD \bot BC\)
Đề bài
Cho tam giác ABC, đường trung trực d1 của đoạn thẳng BC và đường trung trực d2 của đoạn thẳng AC cắt nhau tại O.
a) Chứng minh \(OA = OB = OC.\)
b) Gọi M là trung điểm của đoạn AB. Chứng minh OM là đường trung trực của đoạn AB.
Đề bài
Cho tam giác ABC có \(ID = IE.\) \(\widehat A = {60^o}\), các tia phân giác của góc C, B cắt nhau tại I và cắt AB, AC theo thứ tự ở D và E
Đề bài
Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E. Đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:
a) \(AD = EF \)
b) \(\Delta ADE = \Delta EFC.\)