Bài 16 trang 148 SGK Giải tích 12

Đề bài

Trên mỗi hình 143, 144, 145 có các tam giác vuông nào bằng nhau? Vì sao?

Đề bài

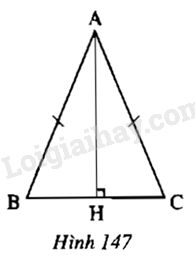
Cho tam giác \(ABC\) cân tại \(A.\) Kẻ \(AH\) vuông góc với \(BC\) (hình 147). Chứng minh rằng \(ΔAHB =ΔAHC\) (giải bằng \(2\) cách)

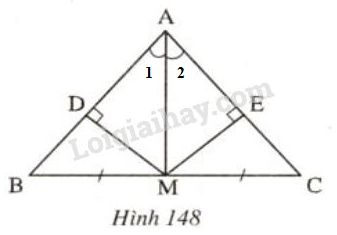
Đề bài

Cho tam giác \(ABC\) cân tại\( A\). Kẻ \(AH\) vuông góc với \(BC\) ( \(H \) thuộc \(BC\)). Chứng minh rằng:

a) \( HB = HC\);

b) \(\widehat{BAH}=\widehat{CAH}\)

Đề bài

Các tam giác vuông \(ABC\) và \(DEF\) có \(\widehat{A}=\widehat{D}= 90^o\), \(AC=DF.\) Hãy bổ sung thêm một điều kiện bằng nhau để \(\Delta ABC=\Delta DEF\).

Đề bài

Cho tam giác \( ABC\) cân tại \( A\) (\(\widehat{A}\)< \(90^o\)). Vẽ \(BH \perp A C\) (\( H\) thuộc \(AC\)), \(CK\perp AB\)  (\( K \) thuộc \(AB\))

a) Chứng minh rằng \( AH = AK.\)

b) Gọi \( I\) là giao điểm của \( BH\) và \( CK\). Chứng minh rằng tia \(  AI \) là tia phân giác của góc \(  A.\)

Đề bài

Tìm các tam giác bằng nhau trên hình 148

Đề bài

Bài 1. Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC, biết AB = 20cm, AH = 12cm, AC = 15cm. Tính BC, BH, CH.

Bài 2. Các tam giác cho dưới đây có phải là tam giác vuông không? Hãy chứng minh, nếu là tam giác vuông cho biết vuông tại đỉnh nào?

a) \(AB = 8cm;\,AC = 17cm;\,BC = 15cm.\)

b) \(AB = 25cm;\,AC = 24cm;\,BC = 6cm.\)

Đề bài

Bài 1. Cho tam giác nhọn ABC, kẻ AH vuông góc với BC \(\left( {H \in BC} \right)\), biết \( \Rightarrow AC = \sqrt {400}  = 20\,(cm)\) \(AB = 13cm;\,AH = 12cm;\,\)\(HC = 16cm\). Tính AC, BC.

Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng cắt hai cạnh AB, AC ở D và E. Chứng minh: \(C{D^2} - C{B^2} = E{D^2} - E{B^2}.\)

Đề bài

Cho tam giac ABC cân tại A, kẻ BH vuông góc với AC. Biết AH= 6cm, CH = 4cm. Tính BC.

Đề bài

Cho tam giác ABC vuông ở A có \(\dfrac{{AB}}{ {AC}} = \dfrac{8 }{ {15}}\) và BC = 51cm.

a) Tính AB, AC.

b) Tính diện tích tam giác ABC

Đề bài

Cho góc nhọn xOy, trên Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A và B kẻ AH, BK lần lượt vuông góc với Oy và Ox.

a) Chứng minh \(\Delta OHA = \Delta OKB.\)

b) Gọi I là giao điểm của AH và BK. Chứng minh rằng OI là phân giác của góc \(\widehat {xOy}.\)

Đề bài

Cho tam giác ABC cân tại A, vẽ BD, CE lần lượt vuông góc với AC và AB. Gọi I là giao điểm cả BD và CE.

a) Chứng minh rằng \(\Delta AEI = \Delta ADI.\)

b) Gọi M là trung điểm của BC. Chứng minh ba điểm A, I, M thẳng hàng.

Đề bài

Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, qua C kẻ tia Cy vuông góc với AC, gọi I là giao điểm của Bx và Cy.

a) Chứng minh \(\Delta ABI = \Delta ACI.\)

b) Chứng tỏ AI là đường trung trực của đoạn BC.

Đề bài

Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^o}} \right)\), các đường trung trực của AB, AC cắt nhau tại O.

a) Chứng minh rằng AO là tia phân giác  của góc A.

b) Kẻ đường vuông góc với AB qua B, kẻ đường vuông góc với AC qua C, chúng cắt nhau tại K. Chứng tỏ ba điểm A, O, K thẳng hàng.

Đề bài

Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC. 

a) Chứng minh \(\Delta AHB = \Delta AHC\)

b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia Cb lấy điểm E sao cho \(BD = CE\). Chứng minh rằng \(\Delta ADE\) cân.