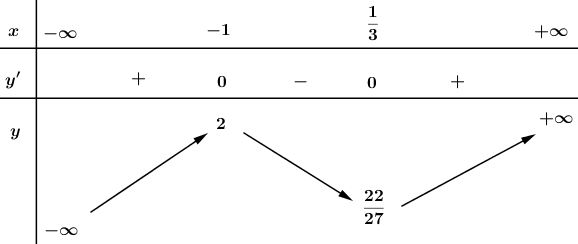
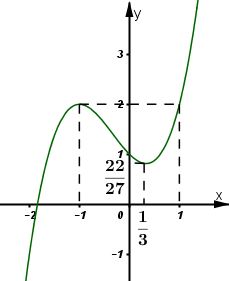
Bài 3 trang 146 SGK Giải tích 12

Đề bài

a) Vẽ hai đường thẳng \(a, b\) sao cho \(a//b\).

b) Vẽ đường thẳng \(c\) cắt \(a\) tại \(A\), cắt \(b\) tại \(B\)

c) Đo một cặp góc so le trong. Nhận xét.

d) Đo một cặp góc đồng vị. Nhận xét.

Đề bài

Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Ơ-clit.

a) Nếu qua điểm \(M\) nằm ngoài đường thẳng \(a\) có hai đường thẳng song song với \(a\) thì chúng trùng nhau.

b) Cho điểm \(M\) ở ngoài đường thẳng \(a\). Đường thẳng đi qua \(M\) song song với đường thẳng \(a\) là duy nhất.

c) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

d) Qua điểm \(M\) nằm ngoài đường thẳng \(a\) có ít nhất một đường thẳng song song với \(a\).

Đề bài

Điền vào chỗ trống (...) trong phát biểu sau:

Nếu một đường thẳng cắt hai đường thẳng song song thì:

a) Hai góc so le trong ...

b) Hai góc đồng vị ...

c) Hai góc trong cùng phía ...

Đề bài

Hình \(22 \) cho biết \(a // b\) và \(\widehat{A_{4}}=37^{\circ}\).

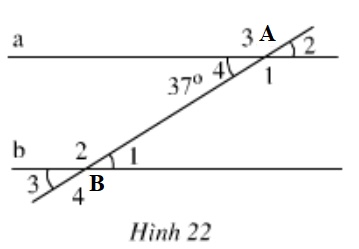
a) Tính \(\widehat{B_{1}}\).

b) So sánh \(\widehat{A_{1}}\) và \(\widehat{B_{4}}\).

c) Tính \(\widehat{B_{2}}\).

Đề bài

Hình \(23\) cho biết \(a // b\) và \(c\) cắt \(a\) tại \(A,\) cắt \(b\) tại \(B.\)

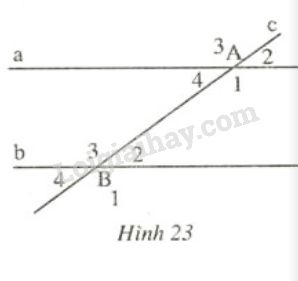
Hãy điền vào chỗ trống (...) trong các câu sau:

a) \(\widehat{A_{1}}=...\) (vì là cặp góc so le trong).

b) \(\widehat{A_{2}}=...\) (vì là cặp góc đồng vị).

c) \(\widehat{B_{3}}+\widehat{A_{4}}=...\) (vì ...).

d) \(\widehat{B_{4}}=\widehat{A_{2}}\) ( vì ...).

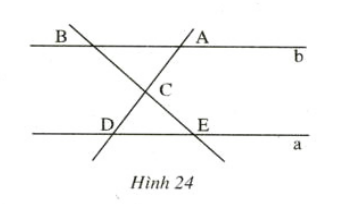
Đề bài

Cho hình \(24\) (\(a // b\)). Hãy nêu tên các cặp góc bằng nhau của hai tam giác \(CAB\) và \(CDE.\)

Đề bài

Hãy điền vào chỗ trống (...) trong bảng sau:

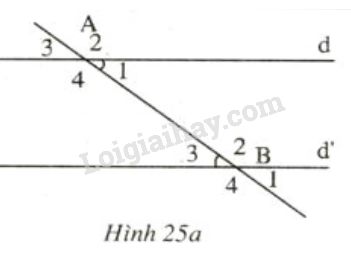
Biết \(d // d'\) (h.25a) thì suy ra: 

a) \(\widehat {{A_1}}\) = \(\widehat {{B_3}}\) và b) ... và c) ...

Nếu một đường thẳng cắt hai đường thẳng song song thì: 

a) ...

b) ...

c) ... 

Biết: (h.25b) 

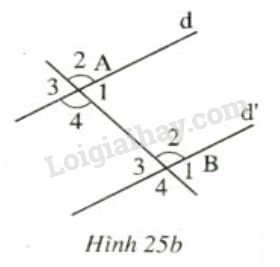
a) \(\widehat {{A_4}}\) = \(\widehat {{B_2}}\) 

hoặc b) ...

hoặc c) ...

thì suy ra \(d // d'\)

 Nếu một đường thẳng cắt hai đường thẳng 

mà a) ...

hoặc b) ...

hoặc c) ...

thì hai đường thẳng đó song song với nhau.

Đề bài

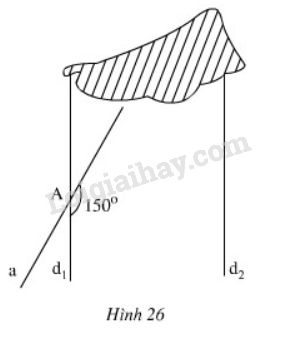
Đố: Hình \(26\) cho biết \({d_1}//{d_2}\) và một góc tù tại đỉnh \(A\) bằng \({150^o}\)

Tính góc nhọn tạo bởi \(a\) và \({d_2}\).

Đề bài

Cho tam giác ABC, qua đỉnh A kẻ đường thẳng a song song với cạnh BC, qua đỉnh B kẻ đường thẳng b song song với cạnh AC.

a)  Vẽ được mấy đường a, mấy đường thẳng b? Vì sao?

b)  Chứng minh rằng a và b cắt nhau.

Đề bài

Bài 1: Cho hình vẽ bên, biết a // b và c cắt a, b lần lượt tại A và B biết \(\widehat {{A_1}} = {54^o}.\)

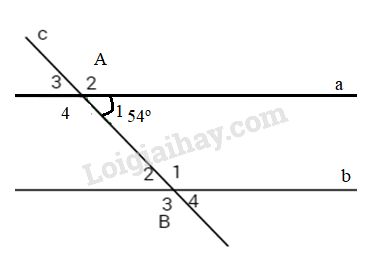
a) Tính \(\widehat {{B_2}}.\)

b) So sánh \(\widehat {{A_4}}\) và \(\widehat {{B_3}}.\)

c) Tính \(\widehat {{A_4}} + \widehat {{B_2}}.\) 

Bài 2:  Cho tam giác ABC, trên cùng nửa mặt phẳng bờ là đường thẳng AB chứa C, vẽ tia AD sao cho \(\widehat {EAB} = \widehat {ACB} \Rightarrow AE//BC.\) \(\widehat {EAB} = \widehat {ABC}\). Chứng tỏ ba điểm E, A, D thẳng hàng.

Đề bài

Bài 1: Cho tam giác ABC. Chứng minh rằng: nếu đường thẳng d song song với BC thì d sẽ cắt các đường thẳng AB và AC.

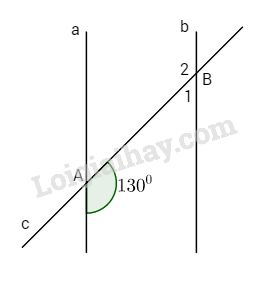
Bài 2: Cho hình vẽ biết a // b và một góc tù tại A bằng 130^o. Tính góc nhọn tạo bởi c và b.

Đề bài

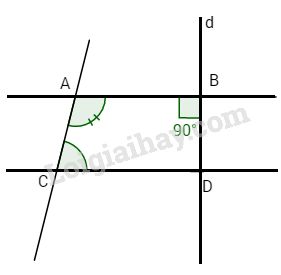
Bài 1: Cho hinh vẽ.

Biết \(\widehat {BAC} + \widehat {ACD} = {180^o}\)và \(d \bot AB.\)Chứng tỏ \(d \bot CD.\)

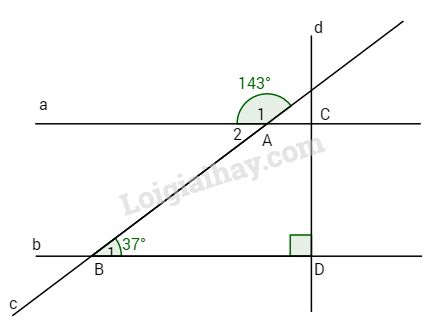
Bài 2: Cho hình vẽ. Biết \(\widehat {{A_1}} = {145^o},\,\widehat B = {37^o}\) và \(d \bot b.\) Hỏi d có vuông góc với a hay không?

Đề bài

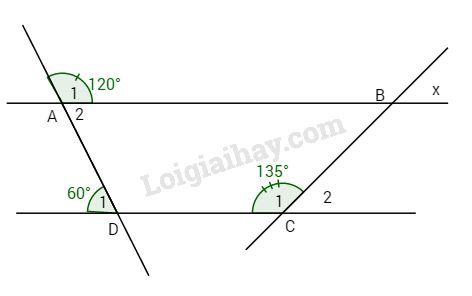
Bài 1: Cho hình vẽ bên.

Biết \(\widehat {{A_1}} = {120^o},\)

\(\widehat {{D_1}} = {60^o},\)

\(\widehat {{C_1}} = {135^o}.\)

Tính \(\widehat {x.}\)

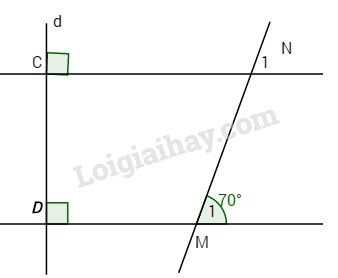
Bài 2:  Cho hình vẽ.

Biết \(CN \bot d,\,DM \bot d.\) Tính \(\widehat {{N_1}}.\)

Đề bài

Cho hình vẽ.

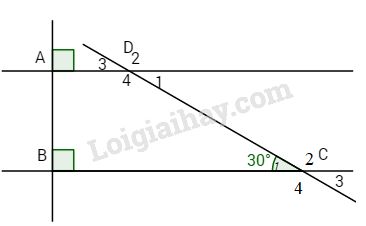
Biết \(\widehat {{D_2}} = \widehat {{C_2}} = {150^o}.\) \(AD \bot AB,\,BC \bot AB\) và \(\widehat {{C_1}} = {30^o}.\)

a) Hỏi AD có song song với BC hay không?

b) Tính các góc \(\widehat C,\,\widehat D\) còn lại.

Đề bài

Cho hình vẽ.

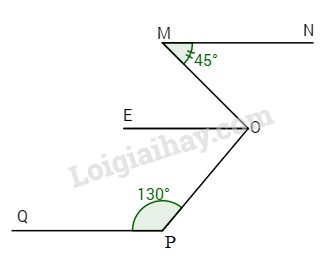
Biết MN // PQ // OE và \(\widehat {MOP} = \widehat {EOP} = {50^o}.\) \(\widehat M = {45^o},\,\widehat P = {130^o}.\)

a) Tính \(\widehat {MOP}.\)

b) Hỏi OE có phải là tia phân giác của \(\widehat {MOP}\) hay không?

c) Trường hợp nếu \(\widehat M = {50^o}\) và \(\widehat P = {130^o}\) thì tia OE có là tia phân giác của góc \(\widehat {MOP}\) không?

Đề bài

Cho hình vẽ.

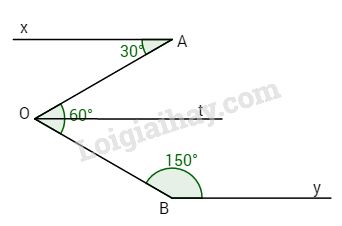
Biết \(\widehat {AOB} = {60^o}\), Ot là phân giác của \(\widehat {AOB}\), \(\widehat A = {30^o},\,\widehat B = {150^o}\). Hỏi các tia Ax, Ot và By có song song với nhau không?

Đề bài

Cho hình vẽ.

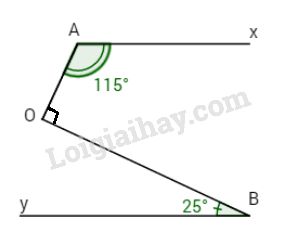
Biết \(\widehat {xAO} = {115^o}\),

\(\widehat {OBy} = {25^o}\),

\(OA \bot BO\).

Chứng minh rằng: Ax // By.

Đề bài

Cho hình vẽ.

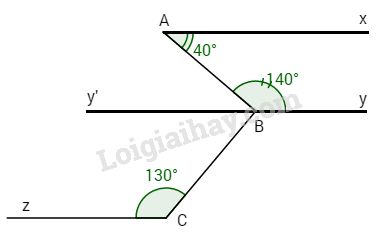
Biết By // Cz.

a) Chứng minh Ax // Cz.

b) Chứng minh \( \Rightarrow \widehat {ABC} = \widehat {ABy'} + \widehat {y'BC} \)\(\;= {40^o} + {50^o} = {90^o}\) \(AB \bot BC\).

Đề bài

Bài 1: Cho hình vẽ.

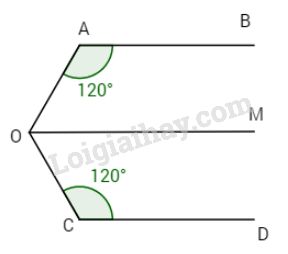
Biết AB // CD // OM và  \(\widehat A = \widehat C = {120^o}\). Hỏi OM có là phân giác của  \(\widehat {AOC}\) hay không?

Biết \(2\widehat x = 3\widehat y\). Tính \(\widehat x;\,\widehat y\).

Bài 2:  Cho hình vẽ.

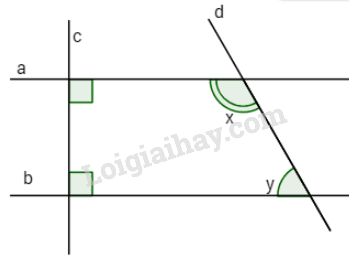
Đề bài

Bài 1: Cho hình vẽ.

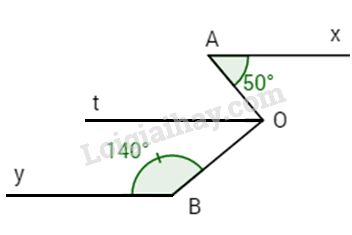
Biết \(\widehat A = {50^o}\),

       \(\widehat B = {140^o}\)

và Ax // By.

Chứng minh rằng \(\widehat {AOB} = {90^o}\).

Bài 2. Cho hình vẽ biết

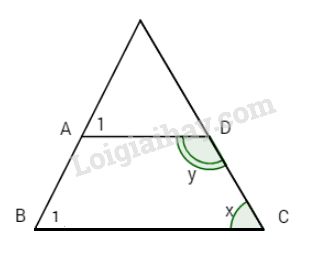
\(\widehat {{A_1}} = \widehat {{B_1}}\) và \(3x = 2y.\) 

Tính x, y.