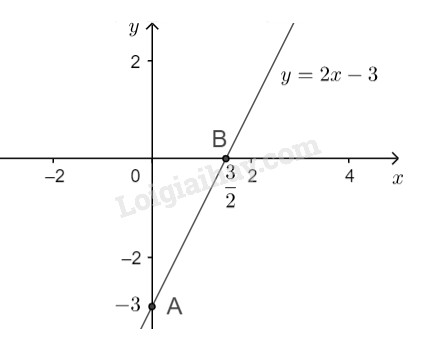
\(a)\) Ta có \(2x - y = 3\)\( \Leftrightarrow y = 2x - 3\)
Nghiệm tổng quát của phương trình đã cho là:
\(\left\{\begin{matrix} x \in {\mathbb{R}} & & \\ y = 2x - 3 & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(y = 2x - 3\) :
Cho \(x = 0 \Rightarrow y = - 3\) ta được \(A(0; -3)\).
Cho \(y = 0 \Rightarrow x = \dfrac{3}{2}\) ta được \(B {\left(\dfrac{3}{2}; 0 \right)}\).
Biểu diễn điểm \(A(0; -3)\) và \(B {\left(\dfrac{3}{2}; 0 \right)}\) trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm \(A,\ B\).
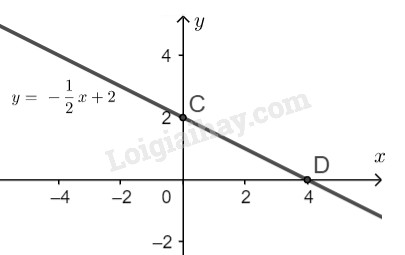
\(b)\) Ta có \(x + 2y = 4 \Leftrightarrow y = \displaystyle - {1 \over 2}x + 2\)
Nghiệm tổng quát của phương trình đã cho là: \(\left\{\begin{matrix} x \in {\mathbb{R}} & & \\ y = \displaystyle - {1 \over 2}x + 2 & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(y = \displaystyle - {1 \over 2}x + 2\) :
Cho \(x = 0 \Rightarrow y = 2\) ta được \(C(0; 2)\).
Cho \(y = 0 \Rightarrow x = 4 \) ta được \(D(4; 0)\).
Biểu diễn điểm \(C(0; 2)\) và \(D(4; 0)\) trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm \(C,\ D\).
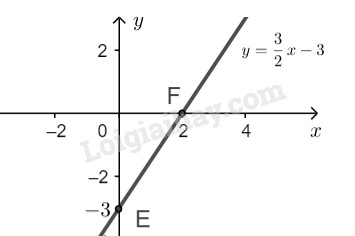
\(c)\) Ta có \(3x - 2y = 6 \Leftrightarrow y = \displaystyle{3 \over 2}x - 3\)
Nghiệm tổng quát của phương trình đã cho là:
\(\left\{\begin{matrix} x \in {\mathbb{R}} & & \\ y = \displaystyle{3 \over 2}x - 3 & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(y = \displaystyle{3 \over 2}x - 3\) :
Cho \(x = 0 \Rightarrow y = -3\) ta được \(E(0; -3)\).
Cho \(y = 0 \Rightarrow x = 2 \) ta được \(F(2; 0)\).
Biểu diễn điểm \(E(0; -3)\) và \(F(2; 0)\) trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm \(E,\ F\).
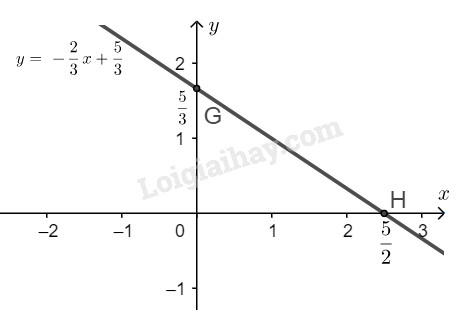
\(d)\)Ta có \(2x + 3y = 5 \Leftrightarrow y = \displaystyle - {2 \over 3}x + {5 \over 3}\)
Nghiệm tổng quát của phương trình đã cho là: \(\left\{\begin{matrix} x \in {\mathbb{R}} & & \\ y = \displaystyle - {2 \over 3}x + {5 \over 3} & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(y = \displaystyle - {2 \over 3}x + {5 \over 3}\) :
Cho \(x = 0 \Rightarrow y = \displaystyle {5 \over 3} \) ta được \(G(0;\dfrac{5}{3})\).
Cho \(y = 0 \Rightarrow x = \displaystyle {5 \over 2} \) ta được \(H(\dfrac{5}{2}; 0)\).
Biểu diễn điểm \(G(0;\dfrac{5}{3})\) và \(H(\dfrac{5}{2}; 0)\) trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm \(G,\ H\).
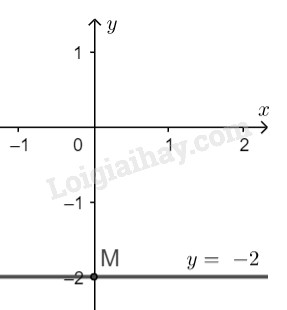
\(e)\) Ta có \(0x + 5y = - 10 \Leftrightarrow y = - 2\)
Nghiệm tổng quát của phương trình đã cho là: \(\left\{\begin{matrix} x \in {\mathbb{R}} & & \\ y = -2 & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(y = - 2\) :
Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(y = - 2\) đi qua điểm \(M(0;-2)\) và song song với trục hoành
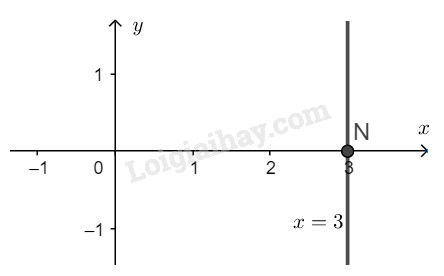
\(f)\) \( - 4x + 0y = - 12 \Leftrightarrow x = 3\)
Nghiệm tổng quát của phương trình đã cho là: \(\left\{\begin{matrix} x=3 & & \\ y \in {\mathbb{R}} & & \end{matrix}\right.\)
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình \(x=3\) :
Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(x = 3\) đi qua điểm \(N(3;0)\) và song song với trục tung.