\(a)\) - Ta có \(2x + y = 1 \Leftrightarrow y = -2x + 1\)
Cho \(x = 0 \Rightarrow y = 1\) ta được \(A(0 ; 1)\)
Cho \(y = 0 \Rightarrow x =\displaystyle {1 \over 2}\) ta được \(B\displaystyle\left( {{1 \over 2};0} \right)\)
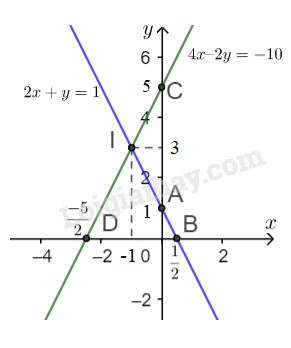
Đường thẳng \(2x + y = 1\) là đường thẳng đi qua hai điểm \(A,\ B\).
- Ta có \(4x – 2y = -10 \Leftrightarrow y = 2x + 5\)
Cho \(x = 0 \Rightarrow y = 5\) ta được \(C(0 ; 5)\)
Cho \(y = 0 \Rightarrow x = \displaystyle - {5 \over 2}\) ta được \(D \displaystyle\left( -{{5 \over 2};0} \right)\)
Đường thẳng \(4x – 2y = -10\) là đường thẳng đi qua hai điểm \(C,\ D\).
- Tìm tọa độ giao điểm:
Hoành độ giao điểm \(I\) của hai đường thẳng \( 2x + y = 1\) và \(4x – 2y = -10\) là nghiệm của phương trình:
\( - 2x + 1 = 2x + 5 \Leftrightarrow 4x = - 4 \\ \Leftrightarrow x = - 1\)
Suy ra tung độ giao điểm \(I\) là \( y = -2 .(- 1) + 1 = 2 + 1 = 3\)
Vậy tọa độ giao điểm của hai đường thẳng đã cho là \( I(-1 ; 3).\)
\(b)\) - Ta có \(0,5x + 0,25y = 0,15\) \( \Leftrightarrow y = -2x + 0,6\)
Cho \(x = 0 \Rightarrow y = 0,6\) ta được \(E(0;0,6)\)
Cho \(y = 0 \Rightarrow x = 0,3\) ta được \(F(0,3;0)\)
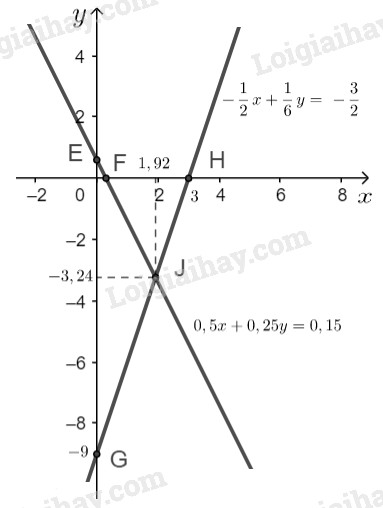
Đường thẳng \(0,5x + 0,25y = 0,15\) là đường thẳng đi qua hai điểm \(E,\ F\).
- Ta có \( \displaystyle - {1 \over 2}x + {1 \over 6}y = - {3 \over 2} \Leftrightarrow y = 3x – 9\)
Cho \(x = 0 \Rightarrow y = - 9\) ta được \(G(0 ; -9)\)
Cho \(y = 0 \Rightarrow x = 3\) ta được \(H(3 ; 0)\)
Đường thẳng \(\displaystyle - {1 \over 2}x + {1 \over 6}y = - {3 \over 2}\) là đường thẳng đi qua hai điểm \(G,\ H\).
- Tìm tọa độ giao điểm:
Hoành độ giao điểm \(J\) của hai đường thẳng \( 0,5x + 0,25y = 0,15\) và \(\displaystyle - {1 \over 2}x + {1 \over 6}y = - {3 \over 2}\) là nghiệm của phương trình:
\(\eqalign{& - 2x + 0,6 = 3x - 9 \Leftrightarrow 5x = 9,6 \cr & \Leftrightarrow x = 1,92 \cr} \)
Suy ra tung độ giao điểm \(J\) là \( y = 3.1,92 – 9 = -3,24\)
Vậy tọa độ giao điểm của hai đường thẳng đã cho là \( J(1,92 ; -3,24).\)
\(c)\) - Ta có \(4x + 5y = 20\) \( \Leftrightarrow y = -0,8x+ 4 \ \ \ (1)\)
Cho \(x = 0 \Rightarrow y = 4\) ta được \(M(0 ; 4)\)
Cho \(y = 0 \Rightarrow x = 5\) ta được \(N(5 ; 0)\)
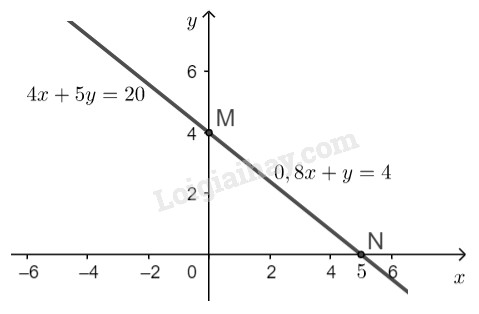
Đường thẳng \(4x + 5y = 20\) là đường thẳng đi qua hai điểm \(M,\ N\).
- Ta có \(0,8x + y = 4\) \( \Leftrightarrow y=-0,8x + 4 \ \ \ (2) \)
- Từ \((1)\) và \((2)\) suy ra hai đường thẳng đã cho trùng nhau. Do đó hai đường thẳng này có vô số điểm chung.
\(d)\) - Ta có \(4x + 5y = 20\) \( \Leftrightarrow y = -0,8x + 4\)
Cho \(x = 0 \Rightarrow y = 4\) ta được \(P(0 ; 4)\)
Cho \(y = 0 \Rightarrow x = 5\) ta được \(Q(5 ; 0)\)
Đường thẳng \(4x + 5y = 20\) là đường thẳng đi qua hai điểm \(P,\ Q\).
- Ta có \(2x + 2,5y = 5\) \( \Leftrightarrow y = -0,8x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được \(R(0 ; 2)\)
Cho \(y = 0 \Rightarrow x = 2,5\) ta được \(S(2,5 ; 0)\)
Đường thẳng \(2x + 2,5y = 5\) là đường thẳng đi qua hai điểm \(R,\ S\).
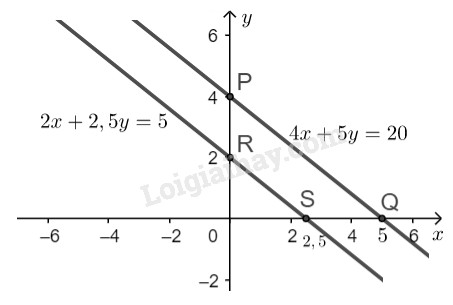
- Hai đường thẳng đã cho có hệ số góc bằng nhau, tung độ gốc khác nhau nên chúng song song với nhau. Do đó hai đường thẳng đã cho không có tọa độ giao điểm.