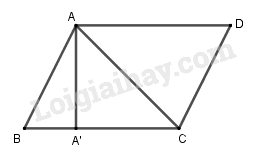
a) Vì ABCD là hình bình hành nên ta có:
\(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \) trong đó \(\overrightarrow {BA} = (5;3)\), \(\overrightarrow {BC} = (6; - 2)\)\( \Rightarrow \overrightarrow {BD} = \left( {11;1} \right)\)
Giả sử D có tọa độ \(({x_D},{y_D})\)
Vì \(\overrightarrow {BD} = (11;1)\) và B(-3; 1) nên ta có: \(\left\{ \begin{array}{l}{x_D} + 3 = 11\\{y_D} - 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = 2\end{array} \right.\)
Chú ý: Ta có thể dựa vào biểu thức vec tơ \(\overrightarrow {AD} = \overrightarrow {BC} \) hoặc \(\overrightarrow {CD} = \overrightarrow {BA} \) để tính tọa độ điểm D.
b) Gọi \(A'\left( {x;y} \right)\) là chân đường cao vẽ từ A ta có: \(\left\{ \begin{array}{l}\overrightarrow {AA'} \bot \overrightarrow {BC} \\\overrightarrow {BA'} = k\overrightarrow {BC} \end{array} \right.\)
Với \(\overrightarrow {AA'} = (x - 2;y - 4),\)\(\overrightarrow {BC} = (6; - 2),\) \(\overrightarrow {BA'} = (x + 3;y - 1)\)
\(\overrightarrow {AA'} \bot \overrightarrow {BC} \Leftrightarrow \overrightarrow {AA'} .\overrightarrow {BC} = 0\) \( \Leftrightarrow 6\left( {x - 2} \right) - 2\left( {y - 4} \right) = 0\)
\(\overrightarrow {BA'} = k\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}x + 3 = 6k\\y - 1 = - 2k\end{array} \right.\) \( \Leftrightarrow \dfrac{{x + 3}}{6} = \dfrac{{y - 1}}{{ - 2}}\) \( \Leftrightarrow - 2\left( {x + 3} \right) = 6\left( {y - 1} \right)\)
Do đó: \(\left\{ \begin{array}{l}\left( {x - 2} \right).6 - 2\left( {y - 4} \right) = 0\\ - 2\left( {x + 3} \right) = 6\left( {y - 1} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}6x - 12 - 2y + 8 = 0\\ - 2x - 6 - 6y + 6 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}6x - 2y - 4 = 0\\ - 2x - 6y = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = \dfrac{3}{5}\\{y_{A'}} = - \dfrac{1}{5}\end{array} \right.\)
\( \Rightarrow A'\left( {\dfrac{3}{5}; - \dfrac{1}{5}} \right)\).