Đường thẳng đi qua gốc tọa độ có dạng \(y = ax + b.\)
a) Vì đường thẳng \(y = ax + b\) đi qua điểm A(2;1) nên tọa độ điểm A nghiệm đúng với phương trình đường thẳng.
Ta có : \(1 = a.2 \Leftrightarrow a = \dfrac{1}{2}\)
Vậy hệ số góc mà đường thẳng đi qua gốc tọa độ và đi qua điểm \(A(2;1)\) là \(a = \dfrac{1}{2}\).
b) Vì đường thẳng \(y = ax\) đi qua điểm \(B(1;-2)\) nên tọa độ điểm \(B\) nghiệm đúng phương trình đường thẳng.
Ta có: \(9 - 2 = a.1 \Leftrightarrow a = - 2\)
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1;-2)
Là \(a = -2.\)
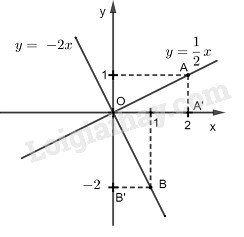
c) Với \(a = \dfrac{1 }{2}\) ta có hàm số: \(y = \dfrac{1 }{2}x\)
Với \(a = -2\) ta có hàm số : \(y = - 2x\)
*) Vẽ đồ thị hàm số \(y = \dfrac{1}{ 2}x\)
Cho \(x = 0\) thì \(y = 0\). Ta có: \(O(0;0)\)
Cho \(x = 2\) thì \(y = 1\). Ta có: \(A(2;1)\)
Đồ thị hàm số \(y = \dfrac{1}{2}x\) đi qua O và A.
*) Vẽ đồ thị hàm số \(y = -2x\)
Cho \(x = 0\) thì \(y = 0\). Ta có : \(O(0;0)\)
Cho \(x = 1\) thì \(y = -2\) . Ta có : \(B(1;-2)\)
Đồ thị hàm số \(y = -2x\) đi qua điểm O và B.
*Gọi A’, B’ lần lượt là hình chiếu của A, B trên Ox, Oy.
Ta có hai tam giác AA’O và BB’O có hai cạnh góc vuông tương ứng bằng nhau nên chúng bằng nhau.
Suy ra : \(\widehat {AOA'} = \widehat {BOB'}\) (1)
Vì \({\rm{Ox}} \bot {\rm{Oy}}\) nên \(\widehat {BOA'} + \widehat {BOB'} = {90^0}\) (2)
Từ (1) và (2) suy ra : \(\widehat {BOA'} + \widehat {AOA'} = {90^0}\)
Vậy \(OA \bot OB\) hay hai đường thẳng \(y = \dfrac{1}{2}x\) và \(y = -2x\) vuông góc với nhau.