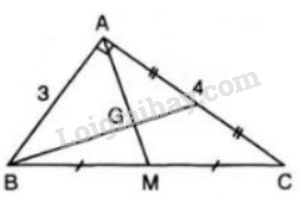
Áp dụng định lí Pitago cho \(∆ABC\) vuông tại \(A\) ta có:
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& B{C^2} = {3^2} + {4^2} = 25 \cr} \)
\(\Rightarrow BC = 5\,cm.\)
Gọi \(M\) là trung điểm của \(BC\) \(\Rightarrow \) \(AM\) là trung tuyến ứng với cạnh huyền \(BC\), do đó \(AM = \dfrac{1}{2} BC\) (1) (Trong một tam giác vuông, đường trung tuyến ứng với cạnh bằng một nửa cạnh huyền).
Vì \(G\) là trọng tâm của \(∆ ABC\) nên \(AG =\dfrac{2}{3} AM\) (2)
Thay (1) vào (2) ta được:
\( AG =\dfrac{2}{3}.\dfrac{1}{2} BC\)
\(\Rightarrow AG = \dfrac{1}{3} BC = \dfrac{1}{3}.5 =\dfrac{5}{3}\,(cm).\)