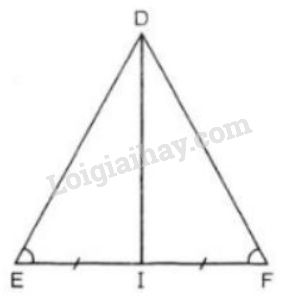
a) Xét \(∆DEI\) và \(∆DFI\) có:
+) \(DI\) là cạnh chung
+) \(DE = DF\) (vì \( ∆DEF\) cân tại \(D\))
+) \(IE = IF\) (\(DI\) là trung tuyến)
Vậy \(∆DEI = ∆DFI\) (c.c.c)
b) Vì \(∆DEI = ∆DFI\) nên \(\widehat{DIE} =\widehat{DIF}\).
Mà \(\widehat{DIE} +\widehat{DIF} = 180^o\) ( hai góc kề bù)
\(\Rightarrow \) \(\widehat{DIE} =\widehat{DIF}= 90^o\)
Vậy các góc \(DIE\) và góc \(DIF\) là những góc vuông.
c) \(I\) là trung điểm của \( EF\) nên \(IE = IF =\dfrac{{EF}}{2} = \dfrac{{10}}{2}= 5\,cm.\)
Áp dụng định lí Pytago vào \(∆DEI\) vuông tại \(I\) ta có:
\(\eqalign{
& D{E^2} = D{I^2} + E{I^2} \cr
& \Rightarrow D{I^2} = D{E^2}-E{I^2} \cr
& \,\,\,\,\,\,\,\,D{I^2}\, = {13^2}-{5^2} = 144 \cr
& \Rightarrow DI = 12\,\,cm \cr} \)