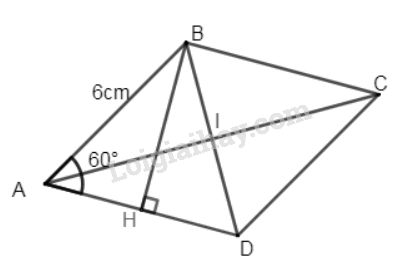
Tính độ dài đường cao BH:
Ta có \(∆ABD\) là tam giác đều (vì tam giác \(ABD\) cân có \(\widehat{A}\) = \(60^{\circ}\) ).
Áp dụng định lí Pytago vào tam giác vuông \(ABH\) có:
\(B{H^2} = A{B^2} - A{H^2}\)
\( = A{B^2}-\left ( \dfrac{AB}{2} \right )^{2}\)
\( = A{B^2}-\dfrac{AB^{2}}{4} = \dfrac{3AB^{2}}{4}\).
\( \Rightarrow BH = \dfrac{AB.\sqrt{3}}2 = \dfrac{6\sqrt{3}}2 = 3\sqrt3\) (cm)
Tổng quát: Đường cao tam giác đều cạnh \(a\) có độ dài là: \({h_a}=\dfrac{a\sqrt{3}}2\)
Tính diện tích hình thoi ABCD.
Cách 1:
Ta có \(∆ABD\) là tam giác đều.
\(BH\) \(\perp\) \(AD\) thì \(HA = HD\) (Trong tam giác đều đường cao đồng thời là trung tuyến).
Suy ra tam giác vuông \(AHB\) là nửa tam giác đều, \(BH\) là đường cao tam giác đều cạnh \(6\,cm\), \(BH = \dfrac{6\sqrt{3}}{2} = 3\sqrt 3\) (cm)
\({S_{ABCD}}= BH. AD = 3\sqrt 3. 6 \)\(\,= 18\sqrt 3\;(c{m^2})\)
Cách 2:
Vì \(∆ABD\) là tam giác đều nên \(BD = AB = 6\,cm\), \(AI\) là đường cao đồng thời là trung tuyến tam giác nên \(AI = \dfrac{6\sqrt{3}}{2} = 3\sqrt3\) (cm)
\(\Rightarrow AC =2AI= 6\sqrt 3\) (cm)
\({S_{ABCD}}=\dfrac{1}{2} BD. AC = \dfrac{1}{2} 6. 6\sqrt 3 \)\(\,= 18\sqrt 3\; (c{m^2})\)