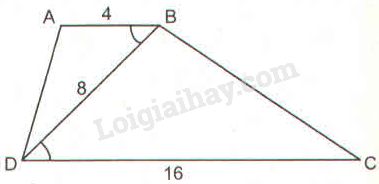
Ta có:
\(\eqalign{ & {{AB} \over {BD}} = {4 \over 8} = {1 \over 2} \cr & {{BD} \over {DC}} = {8 \over {16}} = {1 \over 2} \cr} \)
\( \Rightarrow\displaystyle {{AB} \over {BD}} = {{BD} \over {DC}} = {1 \over 2}\)
Vì \(AB//CD\) (gt) nên \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(∆ ABD\) và \(∆ BDC\) có:
\(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên)
\(\displaystyle{{AB} \over {BD}} = {{BD} \over {DC}}\) (chứng minh trên)
\( \Rightarrow ∆ ABD\) đồng dạng \( ∆ BDC\) (c.g.c)
\( \Rightarrow \widehat {BAD} = \widehat {DBC}\) (hai góc tương ứng).
Tỉ số đồng dạng \(\displaystyle k = {1 \over 2}\).
\( \Rightarrow\displaystyle {{AD} \over {BC}} = {1 \over 2} \Rightarrow BC = 2AD\) (đpcm).