Bài 7. Trường hợp đồng dạng thứ ba (g.g)

Đề bài

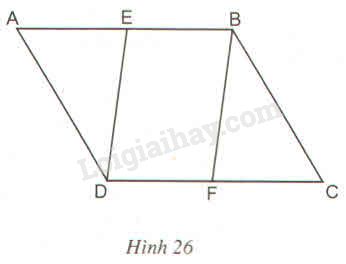
Cho hình bình hành \(ABCD.\) Gọi \(E\) là trung điểm của \(AB,\) \(F\) là trung điểm của \(CD\) (h26). Chứng minh hai tam giác \(ADE\) và \(CBF\) đồng dạng với nhau. 

Đề bài

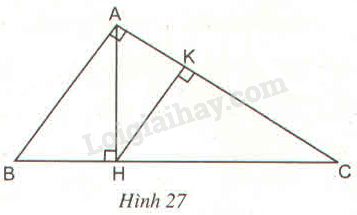
Tam giác vuông \(ABC\) có \(\widehat A = 90^\circ \) và đường cao \(AH.\) Từ điểm \(H\) hạ đường \(HK\) vuông góc với \(AC\) (h.27).

a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.

Đề bài

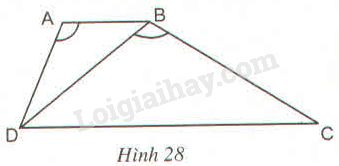
Hình thang \(ABCD (AB // CD)\) có \(AB = 2,5cm, AD = 3,5cm,\) \(BD = 5cm\) và \(\widehat {DAB} = \widehat {DBC}\)  (h.28).

a) Chứng minh \(∆ ADB\backsim ∆ BCD.\)

b) Tính độ dài các cạnh \(BC, CD\).

c) Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.

Đề bài

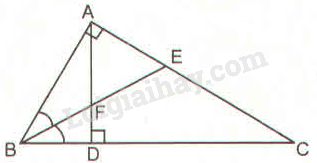
Cho tam giác vuông \(ABC\) (\(\widehat A = 90^\circ \)). Dựng \(AD\) vuông góc với \(BC\) (\(D\) thuộc \(BC\)). Đường phân giác \(BE\) cắt \(AD\) tại \(F\) (h.29).

Chứng minh: \(\displaystyle {{FD} \over {FA}} = {{EA} \over {EC}}\). 

Đề bài

Chứng minh rằng, nếu hai tam giác \(ABC\) và \(A’B’C’\) đồng dạng với nhau thì:

a) Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng.

b) Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng.

Đề bài

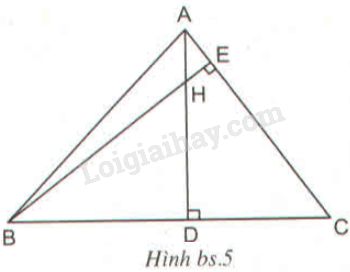
Hình bs.5 cho biết tam giác \(ABC\) có hai đường cao \(AD\) và \(BE \) cắt nhau tại \(H.\)

Trong hình bs.5 có số cặp tam giác đồng dạng với nhau là:

A. 1 cặp                   B. 2 cặp

C. 3 cặp                   D. 4 cặp 

Hãy chọn kết quả đúng.

Đề bài

Hình thang vuông \(ABCD (AB // CD)\) có đường chéo \(BD\) vuông góc với cạnh \(BC\) tại \(B\) và có độ dài \(BD = m = 7,25cm.\)

Hãy tính độ dài các cạnh của hình thang, biết rằng \(BC = n = 10,75cm.\)

(Tính chính xác đến hai chữ số thập phân).