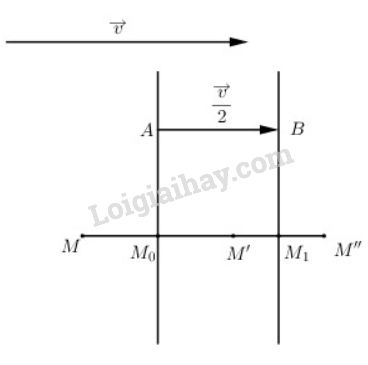
Lấy A bất kì thuộc đường thẳng d, xác định điểm B sao cho \(\overrightarrow {AB} = {{\overrightarrow v } \over 2}\), qua B kẻ đường thẳng d’ // d. Khi đó d’ chính là ảnh của đường thẳng d qua phép tịnh tiến theo vector \({{\overrightarrow v } \over 2}\).
Lấy M là một điểm bất kì, gọi \(M' = {D_d}\left( M \right);\,\,M'' = {D_{d'}}\left( {M'} \right)\)
Gọi \({M_0} = MM' \cap d;\,\,{M_1} = M'M'' \cap d' \Rightarrow {M_0}\) và \({M_1}\) lần lượt là trung điểm của \(MM'\) và \(M'M''\).
Ta có \(\overrightarrow {MM'} = 2\overrightarrow {{M_0}M'} ;\,\,\overrightarrow {M'M''} = 2\overrightarrow {M'{M_1}} \)
\(\eqalign{ & \Rightarrow \overrightarrow {MM''} = \overrightarrow {MM'} + \overrightarrow {M'M''} = 2\overrightarrow {{M_0}M'} + 2\overrightarrow {M'{M_1}} \cr & = 2\left( {\overrightarrow {{M_0}M'} + \overrightarrow {M'{M_1}} } \right) = 2\overrightarrow {{M_0}{M_1}} = 2\overrightarrow {AB} \cr&= \overrightarrow v \cr & \Rightarrow {T_{\overrightarrow v }}\left( M \right) = M'' \cr} \)
Vậy phép tịnh tiến theo vector \(\overrightarrow v \) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).