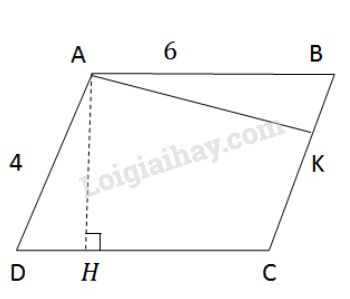
Cho hình bình hành \(ABCD\). Gọi \(AH, AK\) lần lượt là đường cao kẻ từ \(A\) đến \(CD, BC.\)
Ta có: \({S_{ABCD}} = AB.AH = AD.AK\)
\({S_{ABCD}} = 6.AH = 4.AK\)
Xét \(\Delta ABK\) vuông tại \(K\) nên \(AK<AB\) do đó \(AK < 6\).
Xét \(\Delta ADH\) vuông tại \(H\) nên \(AH<AD\) do đó \(AH<4\).
Đường cao có độ dài \(5 \,cm\) thì đó là \(AK\), không thể là \(AH\) vì \(AH < 4.\)
Vậy \(6.AH = 4.5 = 20 \)
\(\Rightarrow AH = \dfrac{{20}}{6}=\dfrac{{10}}{3}\,\,\left( {cm} \right)\)