a) Ta có:
\(\left\{ \matrix{
2x - y = 1 \hfill \cr
x - 2y = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = 2x - 1 \ (d)\hfill \cr
y = \dfrac{1}{2}x + \dfrac{1}{2} \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=2x-1\)
Cho \(x = 0 \Rightarrow y = -1\), ta được \(A(0; -1)\).
Cho \(y = 0 \Rightarrow x = \dfrac{1}{2}\), ta được \(B{\left(\dfrac{1}{2}; 0 \right)}\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(A,\ B\).
+) Vẽ \((d')\): \(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
Cho \(x = 0 \Rightarrow y = \dfrac{1}{2}\), ta được \(C {\left(0; \dfrac{1}{2} \right)}\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D = (-1; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(C,\ D\).
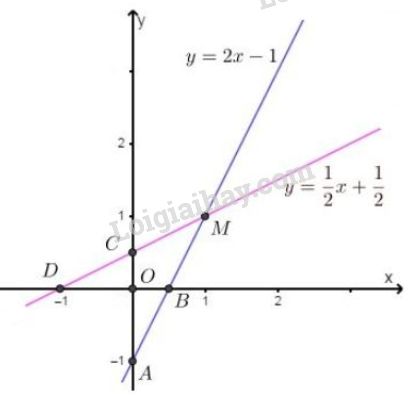
+) Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(M( 1, 1)\).
Thay \(x = 1, y = 1\) vào các phương trình của hệ ta được:
\(\left\{ \begin{array}{l}2x - y = 1\\x - 2y = - 1\end{array} \right.\)
\(\Rightarrow\left\{ \begin{array}{l}2.1 - 1 = 1\\1 - 2.1 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = 1\\ - 1 = - 1\end{array} \right.\) (luôn đúng)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 1)\).
b) Ta có:
\(\left\{ \matrix{ 2x + y = 4 \hfill \cr - x + y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = - 2x + 4 \ (d) \hfill \cr y = x + 1 \ (d') \hfill \cr} \right.\)
+) Vẽ \((d)\): \(y=-2x+4\)
Cho \(x = 0 \Rightarrow y = 4\), ta được \(A(0; 4)\).
Cho \(y = 0 \Rightarrow x = 2\), ta được \(B(2; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(A,\ B\).
Vẽ \((d')\): \(y=x+1\)
Cho \(x = 0 \Rightarrow y = 1\), ta được \(C(0; 1)\).
Cho \(y = 0 \Rightarrow x = -1\), ta được \(D(-1; 0)\).
Tập nghiệm của phương trình là đường thẳng đi qua hai điểm \(C,\ D\).

Quan sát hình vẽ, ta thấy hai đường thẳng cắt nhau tại điểm có tọa độ \(N(1;2)\).
Thay \(x = 1, y = 2\) vào các phương trình của hệ ta được:
\(\left\{ \begin{array}{l}2x + y = 4\\ - x + y = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2.1 + 2 = 4\\ - 1 + 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 = 4\\1 = 1\end{array} \right.\) (luôn đúng)
Vậy hệ phương trình có một nghiệm \((x; y) = (1; 2)\).