a) \(∆ABC\) có \(AC = AB\), \(\hat A = {90^o}\) nên vuông cân tại \(A.\)
\( \Rightarrow \) \(\widehat {ACB} = {45^o}\)
Mà \(∆BCD\) cân tại \(C\) (do \(BC = CD\)) có \(\widehat {ACB}\) là góc ngoài tại \(C\) nên
\(\widehat {ACB} = 2{\rm{x}}\)
\( \Rightarrow x = \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}.{45^o}\)
\(\Rightarrow x = {22^o}30'\).
b) Vẽ tia \(Cx // BA\) (\(BA, Cx\) thuộc hai nửa mặt phẳng đối nhau có bờ \(BC\))
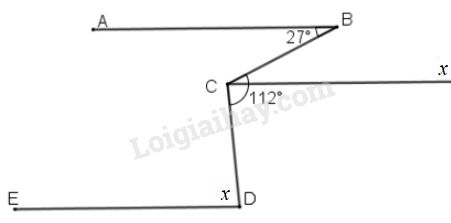
\( \Rightarrow\) \(\widehat {ABC} = \widehat {BCx} = {27^o}\) (hai góc ở vị trí so le trong)
Mà \(\widehat {xCD} = \widehat {BCD} - \widehat {BCx} = {112^o} - {27^o}\)\( = {85^o}\)
Vì \(Cx //ED\) (vì cùng song song \(AB\))
\(\Rightarrow \) \(\widehat {CDE} = \widehat {xCD} = {85^o}\) (hai góc ở vị trí so le trong)
Vậy \( x = {85^o}\)
c) Vì \(AB // CD\) \(\Rightarrow \) \(\widehat {BAC} = \widehat {DCy} = {67^o}\) (hai góc đồng vị)
\(∆ABC\) cân tại \(B\) (do \(AB = BC\)) nên \( \widehat {ABC} = {180^o} - 2\widehat {BAC} = {180^o} - {2.67^o}\)\( = {46^o}\).
Vậy \( x = 46^o\).