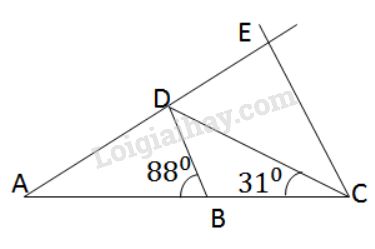
a) \(∆ADC\) cân tại \(D\) nên có \(\widehat {ACD} =\hat A = {31^o} \)
\(\Rightarrow \; \widehat {ADC} = {180^o} - 2. \widehat {ACD}\)
\(\Rightarrow \) \(\widehat {ADC} = {180^o} - 2.{31^o} = {118^o}\)
+ \(∆ADB\) có \(\hat A = {31^o},\widehat {ABD} = {88^o}\)
\(\Rightarrow \) \(\widehat {ADB} = {180^o} - \left( {{{31}^o} + {{88}^o}} \right)\) (định lí tổng ba góc trong tam giác )
Hay \(\widehat {ADB} = {61^o}\)
+ Ta có \(BD // CE\)
\(\Rightarrow \) \(\widehat {DEC} = \widehat {ADB} = {61^o}\) (hai góc đồng vị)
+ \(\widehat {EDC}\) là góc ngoài \(∆ADC\) cân tại \(D\)
\(\Rightarrow \) \(\widehat {EDC} = 2.\hat C = {62^o}\)
\(∆DEC\) có \(\widehat {DEC} = {61^o};\widehat {EDC} = {62^o} \)
Theo định lí tổng ba góc trong một tam giác ta có:
\(\widehat {DCE} = {180^o} - (\widehat {DEC} + \widehat {EDC}) \)
\(= 180^o - (61^o + 62^o)= {57^0}\)
b) Vì \({57^0} < {61^0} < {62^0} \Rightarrow DE < DC < CE\) (Theo định lí mối quan hệ giữa góc và cạnh đối diện trong tam giác).
Vậy \(CE\) là cạnh lớn nhất.