LG a
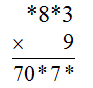
Ở số hàng đơn vị: \(9.3=27.\) Như vậy chữ số hàng đơn vị là \(7\) và nhớ \(2) sang hàng chục.
Ở số hàng chục ta có: \(9 \times * +2\) có chữ số tận cùng bằng \(7\), nên \(9\times*\) có chữ số tận cùng bằng \(5.\)
Suy ra chữ số hàng chục của thừa số đầu tiên là \(5.\)
Chữ số hàng trăm của tích là \(6( 9 . 8 + 4 = 76) \)
Ở hàng nghìn ta có: \(9 . * + 7 = 70\) nên \(9 . *\) có chữ số tận cùng bằng \(3.\)
Suy ra chữ số hàng nghìn của số bị nhân là \(7.\)
Vậy ra có phép tính:
LG b
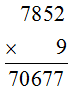
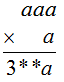
Vì \(a.a\) có chữ số tận cùng bằng \(a\) nên \(a \in \{ 0;1;5;6\}\)
Vì tích \(aaa.a\) là một số có bốn chữ số nên \(a > 3\)
Ta có \(555.5 = 2775 < 3000\) ( loại )
\(666.6 = 3996\) (thỏa)
Vậy ta có phép tính:
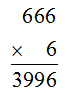
Phương pháp giải - Làm tính nhân từ phải sang trái, căn cứ vào những hiểu biết về tính chất của số tự nhiên và của phép tính, suy luận từng bước để tìm ra những số chưa biết.
- Làm tính nhân từ phải sang trái, căn cứ vào những hiểu biết về tính chất của số tự nhiên và của phép tính, suy luận từng bước để tìm ra những số chưa biết.