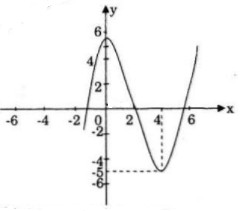
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
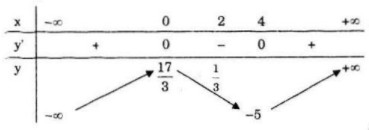
& y'\left( x \right) = {x^2} - 4x;\,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 4 \hfill \cr} \right.;\,f\left( 0 \right) = {{17} \over 3};\,f\left( 4 \right) = - 5 \cr} \)
\(\eqalign{
& f''\left( x \right) = 2x - 4;\,f''\left( x \right) = 0 \Leftrightarrow x = 2 \cr
& f\left( 2 \right) = {1 \over 3} \cr} \)
Điểm uốn \(I\left( {2;{1 \over 3}} \right)\)
Đồ thị nhận I làm tâm đối xứng.
b) Hàm số đã cho có cực đại và cực tiểu và giá tị cực đại, cực tiểu trái dấu, tức hai điểm cực đại và cực tiểu của đồ thị nằm về hai phía đối với trục hoành do đó đồ thị hàm số cắt trục hoành tại ba điểm phân biệt