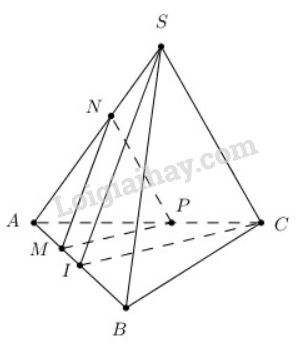
Tam giác ABC đều cạnh \(\displaystyle a \Rightarrow IC = {{a\sqrt 3 } \over 2}\)
Ta có: \(\dfrac{{AM}}{{AI}} = \dfrac{{MP}}{{IC}} \) \(\Rightarrow MP = \dfrac{{AM.IC}}{{AI}} = \dfrac{{x.\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = x\sqrt 3 \)
\( \Rightarrow MP = MN = x\sqrt 3 \)
Áp dụng định lí Ta-let trong tam giác SAC có \(\displaystyle {{NP} \over {SC}} = {{AP} \over {AC}} = {{AM} \over {AI}}\) \( \displaystyle \Rightarrow NP = SC.{{AM} \over {AI}} = a.{x \over {{a \over 2}}} = 2x\)
Vậy chu vi tam giác MNP bằng \(MN + MP + NP = x\sqrt 3 + x\sqrt 3 + 2x \) \(= 2x\left( {1 + \sqrt 3 } \right)\)
Chọn đáp án B.