Bài 1.
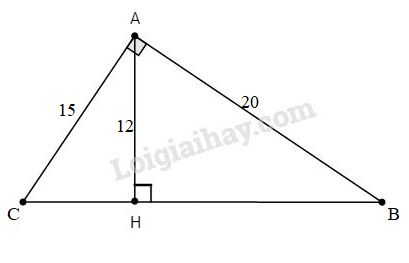
\(\Delta ABC\) vuông tại A ta có \(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{ & = {20^2} + {15^2} \cr & = 625 \cr} \)
\( \Rightarrow B{C^2} = \sqrt {625} = 25\,(cm)\)
Lại có \(AH \bot BC\) (giả thiết) nên \(\Delta AHB\) vuông tại H.
Ta có \(B{H^2} = A{B^2} + A{H^2}\)\(\, = {20^2} + {12^2} = 256\)
\( \Rightarrow BH = \sqrt {256} = 16\,(cm)\)
Do đó \(CH = BC - BH= 25 - 16 = 9\,(cm)\)
Bài 2.
a) Ta có \({8^2} + {15^2} = {17^2}\,(A{B^2} + B{C^2} = C{A^2})\). Theo định lí Pytago đảo ta có \(\Delta ABC\) vuông tại B.
b) Ta có \({6^2} + {24^2} \ne {25^2}\).
Vậy \(\Delta ABC\) không phải là tam giác vuông.