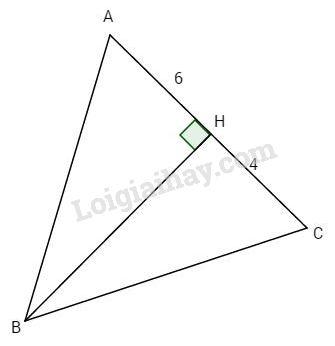
\(\Delta ABC\) cân tại A nên \(AB = AC = AH + HC = 6 + 4 = 10\)(cm).
\(BH \bot AC\) (giả thiết). Do đó \(\Delta AHB\) vuông tại H. Khi đó
\(B{H^2} = A{B^2} - A{H^2}\) (định lý Pytago)
\(\;\;\;\;\;\;\;\;\; = {10^2} - {6^2} = 64\,(c{m^2})\)
Xét tam giác vuông BHC ta có:
\(B{C^2} = B{H^2} + H{C^2}\)
\( \;\;\;\;\;\;\;\;= 64 + {4^2} = 80\,(c{m^2})\)
\( \Rightarrow BC = \sqrt {80} \,(cm).\)