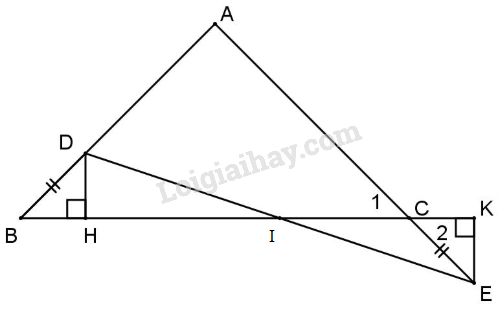
a) Ta có \(\widehat B = {\widehat C_1}\) (gt) và \({\widehat C_1} = {\widehat C_2}\) (đối đỉnh) \( \Rightarrow \widehat B = {\widehat C_2}\).
Do đó hai tam giác vuông \(\Delta BH{\rm{D}} = \Delta CKE\) (ch.gn)
\( \Rightarrow BH = CK\).
b) Ta có \(BC = BH + HC\)
\(HK + HC + CK\), mà \(HB = CK\) (cmt)
\( \Rightarrow BC = HK\).
Ta có \(\Delta DHI\) vuông tại H nên \(HI < DI\)
Tương tự \(IK < IE\)
\( \Rightarrow HI + IK < DI + IE\)
Hay \(HK < DE\), mà \(HK = BC\), do đó \(BC < DE\).