Bài 1: Gọi x, y, z là ba số cần tìm. Ta có \(x + y + z = 90\)
Vì x, y, z tỉ lệ nghịch với 3,4,6 nên ta có \(3x = 4y = 6z\)
\( \Rightarrow {x \over {{1 \over 3}}} = {y \over {{1 \over 4}}} = {z \over {{1 \over 6}}} = {{x + y + z} \over {{1 \over 3} + {1 \over 4} + {1 \over 6}}} = {{90} \over {{3 \over 4}}} = 120\)
\( \Rightarrow x = {{120} \over 3} = 40;y = {{120} \over 4} = 30;\)\(\;z = {{120} \over {60}} = 20.\)
Vậy ba số cần tìm là : 40 ; 30 ; 20.
Bài 2: Gọi x, y, z là số học sinh giỏi, khá, trung bình cần tìm ; \(x,y,z \in {\mathbb N^*}\) .
Vì x, y, z tỉ lệ thuận với 2 ; 5 ; 6 nên ta có : \({x \over 2} = {y \over 5} = {z \over 6} = 45\)
\(\Rightarrow x = 90;y = 225;z = 270\) \({x \over 2} = {y \over 5} = {z \over 6} = {{x + y - z} \over {2 + 5 - 6}}.\)
Theo điều kiện của bài toán : Tổng số học sinh giỏi, khá nhiều hơn số học sinh trung bình là 45 em nên : \(x + y - z = 45\)
Vậy Số học sinh giỏi , khá, trung bình lần lượt là 90 ; 225 ; 270 (em)
Bài 3:
a) Đồ thị của hàm số \(y = -2x\) là đường thẳng qua gốc tọa độ O và điểm \(I(1 ;-2)\) (xem hình vẽ).
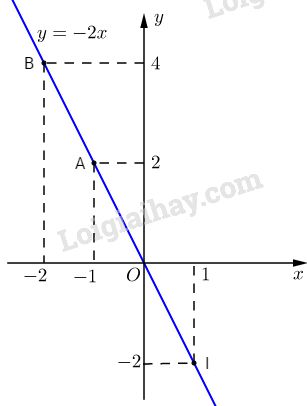
b) Thế tọa độ của M :\({x_M} = 0;{y_M} = - 2\) vào công thức \(y = -2x\), ta được :
\(2=(-2).0\) (sai)
Vậy M không thuộc đồ thị.
c) Thế tọa độ của A: \({x_A} = - 1;{y_A} = 2\) vào công thức \(y = 2x\) ta được:
\(-2 = (-2).(-1)\) ( luôn đúng).
Vậy A nằm trên đồ thị của hàm số \(y = -2x.\)
Tương tự đối với điểm B. Theo trên O cũng là điểm thuộc đồ thị và đồ thị là đường thẳng nên có có thể nói O ; A ; B thẳng hàng.