Bài 1: Học sinh yếu chiếm \({1 \over 8}\) số học sinh nên số học sinh yếu là ta có :
\(496.{1 \over 8} = 62\)(em).
Vậy số học sinh còn lại : \(496 - 62 = 434\) học sinh giỏi, khá và trung bình.
Gọi x, y, z là số học sinh giỏi, khá và trung bình (\(x,y,z \in {\mathbb N^*}\) ). Với x, y, z tỉ lệ ( thuận ) với 7 ; 10 ; 14 nên ta có:
\({x \over 7} = {y \over {10}} = {z \over {14}} = {{x + y + z} \over {7 + 10 + 14}} = {{434} \over {31}} = 14\)
\( \Rightarrow x = 14.7 = 98;y = 14.10 = 140;\)\(\;z = 14.14 = 196.\)
Trả lời : Số học sinh giỏi, khá, trung bình, yếu lần lượt là 98 ;140 ;196 ;62 (em)
Bài 2: Gọi x là vận tốc (x > 0 ; km/h ); y là thời gian (y > 0; giờ).
Ta có thể tóm tắt trong bảng như sau:
|
|
Xe I
|
Xe II
|
|
x
|
\({x_1} = 60\)
|
\({x_2} = 40\)
|
|
y
|
\({y_1}\)
|
\({y_2}\)
|
Ta có : \({x_1}{y_1} = {x_2}{y_2}\) (quãng đường AB).
\( \Rightarrow {{{y_1}} \over {{x_2}}} = {{{y_2}} \over {{x_1}}}\) hay \({{{y_1}} \over {40}} = {{{y_2}} \over {60}} = {{{y_2} - {y_1}} \over {60 - 40}} = {{{1 \over 2}} \over {20}} = {1 \over {40}}\) \( 30 phút = {1 \over 2}\) (giờ)
\( \Rightarrow {y_1} = 1\)(giờ)
Vậy \({x_1}.{y_1} = 60.1 = 60\)
Vậy quãng đường AB dài 60km
Bài 3:
a) Ta có : \(f( - 1) = {1 \over 2} \Rightarrow m.( - 1) = {1 \over 2} \)
\(\Rightarrow m = - {1 \over 2}.\)
Vậy \(y = f(x) = - {1 \over 2}x\).
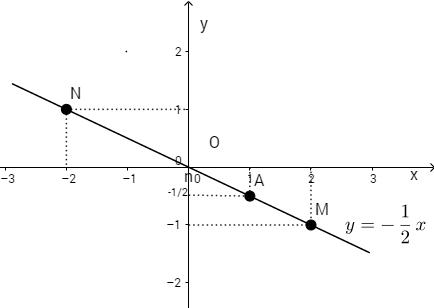
b) Đồ thị của hàm số \(y = - {1 \over 2}x\) là đường thẳng qua gốc tọa độ và điểm \(A\left( {1;{1 \over 2}} \right).\) (xem hình vẽ)
c) Thế tọa độ của M : \({x_M} = 2;{y_M} = - {1 \over 2}x\) ta được : \( - 1 = \left( { - {1 \over 2}} \right).2\) (luôn đúng).
Vậy M thuộc đồ thị của hàm số \(y = - {1 \over 2}x.\)
Tương tự N cũng thuộc đồ thị này, mà đồ thị là đường thẳng đi qua O. Vậy O ; M ; N thẳng hàng.