Hàm số \(f(x) = \left\{ {\begin{array}{*{20}{c}}{ - 2x;x \ge 0}\\{\sin \dfrac{x}{2};x < 0}\end{array}} \right.\) không có đạo hàm tại \(x = 0\) vì:
+) \(\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{f(x) - f(0)}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{ - 2x}}{x} = - 2\),
+) \(\mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{f(x) - f(0)}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{\sin \dfrac{x}{2}}}{x} \) \(= \mathop {\lim }\limits_{x \to {0^ - }} \dfrac{{\sin \dfrac{x}{2}}}{{2.\dfrac{x}{2}}} = \dfrac{1}{2}\)
Mặt khác, với \(x < 0\;\) thì \(y' = \dfrac{1}{2}\cos \dfrac{x}{2}\), với \(x > 0\) thì \(y' = - 2 < 0\)
Xét trên khoảng \(\left[ { - \pi ;\pi } \right]\) ta có bảng biến thiên:
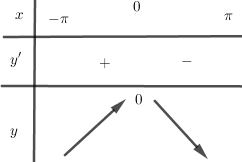
Từ đó ta thấy hàm số đạt cực đại tại \(x = 0\) và \({y_{CD}} = y\left( 0 \right) = 0\).