Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Khảo sát và vẽ đồ thị các hàm số:

a) \(y = 2 - 3x - {x^2}\)

b) \(y = {x^3} - {x^2} + x\)

c) \(y =  - {x^4} + 2{x^3} + 3\)

Khảo sát và vẽ đồ thị các hàm số:

a) \(y = \dfrac{{x - 2}}{{x + 1}}\)        b) \(y = \dfrac{{2 - x}}{{2x - 1}}\)

Tìm giá trị của tham số \(m\) để hàm số

a) \(y = {x^3} + (m + 3){x^2} + mx - 2\) đạt cực tiểu tại \(x = 1\)

b) \(y =  - \dfrac{1}{3}({m^2} + 6m){x^3} - 2m{x^2} + 3x + 1\)  đạt cực đại tại \(x =  - 1\)

Tìm giá trị của tham số \(m\) để hàm số \(y = (m - 1){x^4} - m{x^2} + 3\)  có đúng một cực trị.

Cho hàm số: \(y = \dfrac{1}{4}{x^3} - \dfrac{3}{2}{x^2} + 5\)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho

b) Tìm các giá trị của tham số \(m\) để phương trình \({x^3}-6{x^2} + m = 0\;\) có \(3\) nghiệm thực phân biệt.

(Đề thi tốt nghiệp THPT năm 2010)

a) Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số:  \(y =  - {x^3} + 3x + 1\)

b) Chỉ ra phép biến hình biến \(\left( C \right)\) thành đồ thị \(\left( {C'} \right)\) của hàm số: \(y = {(x + 1)^3} - 3x - 4\)

c) Dựa vào đồ thị \(\left( {C'} \right)\), biện luận theo \(m\) số nghiệm của phương trình: \({(x + 1)^3} = 3x + m\)

d) Viết phương trình tiếp tuyến \(\left( d \right)\) của đồ thị \(\left( {C'} \right)\), biết tiếp tuyến đó vuông góc với đường thẳng \(y =  - \dfrac{x}{9} + 1\)

Biện luận theo k số nghiệm của phương trình:

a) \({(x - 1)^2} = 2|x - k|\)

b) \({(x + 1)^2}(2 - x) = k\)

Cho hàm số: \(y = {x^3} - (m + 4){x^2} - 4x + m\)   (1)

a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của \(m\).

b) Chứng minh rằng với mọi giá trị của \(m\), đồ thị của hàm số (1) luôn luôn có cực trị.

c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi \(m = 0\)

d) Xác định \(k\) để (C) cắt đường thẳng \(y = kx\) tại ba điểm phân biệt.

Cho hàm số \(y = 2{x^4} - 4{x^2}\)(1)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).

b) Với giá trị nào của \(m\), phương trình  \({x^2}|{x^2} - 2| = m\) có đúng \(6\) nghiệm thực phân biệt?

(Đề thi đại học năm 2009; khối B)

Cho hàm số: \(y = \dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4}\)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của (C) tại các giao điểm của nó với trục \(Ox\).

c) Biện luận theo \(k\) số giao điểm của (C) với đồ thị (P) của hàm số: \(y = k-2{x^2}\).

LG câu a

Phương pháp:

Khảo sát tóm tắt:

- Tìm TXĐ, tính đạo hàm \(y'\).

- Lập bảng biến thiên và vẽ đồ thị hàm số.

Cách giải:

Tập xác định: \(D = \mathbb{R}\).

Có \(y' = {x^3} - 4x;\) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 2\end{array} \right.\).

Bảng biến thiên:

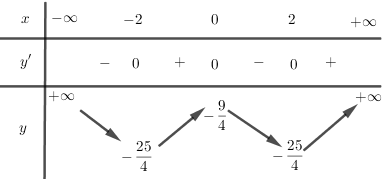
Đồ thị:

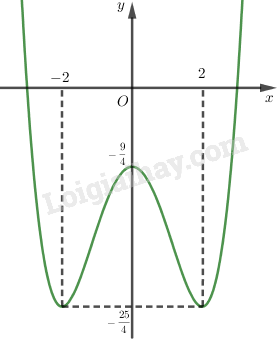
LG câu b

Phương pháp:

- Giải phương trình hoành độ giao điểm.

- Tìm tọa độ giao điểm của \(\left( C \right)\) với \(Ox\).

- Viết phương trình tiếp tuyến theo công thức \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\).

Cách giải:

\(\dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4} = 0\)\( \Leftrightarrow {x^4} - 8{x^2} - 9 = 0\)\( \Leftrightarrow ({x^2} + 1)({x^2} - 9) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x = 3\end{array} \right.\)
Nên \(\left( C \right)\) cắt \(Ox\) tại hai điểm \(\left( { - 3;0} \right)\) và \(\left( {3;0} \right)\).

Ta có: \(y' = {x^3} - 4x \Rightarrow \left\{ \begin{array}{l}y'\left( 3 \right) = 15\\y'\left( { - 3} \right) =  - 15\end{array} \right.\)

Phương trình tiếp tuyến của (C) tại điểm \(\left( {3;0} \right)\) là \(y = 15\left( {x - 3} \right) + 0\) hay \(y = 15x - 45\).

Phương trình tiếp tuyến của (C) tại điểm \(\left( { - 3;0} \right)\) là \(y =  - 15\left( {x + 3} \right) + 0\) hay \(y =  - 15x - 45\).

LG câu c

Phương pháp:

- Xét phương trình hoành độ giao điểm.

- Biện luận số giao điểm theo số nghiệm của phương trình và kết luận.

Cách giải:

Xét phương trình hoành độ giao điểm:

\(\dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4} = k - 2{x^2}\)\( \Leftrightarrow {x^4} = 9 + 4k\,\,\left( * \right)\)

+) Nếu \(9 + 4k > 0 \Leftrightarrow k >  - \dfrac{9}{4}\) thì \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}{x^2} = \sqrt {9 + 4k} \\{x^2} =  - \sqrt {9 + 4k} \left( L \right)\end{array} \right.\)\( \Leftrightarrow x =  \pm \sqrt[4]{{9 + 4k}}\) hay \(\left( * \right)\) có hai nghiệm phân biệt.

+) Nếu \(9 + 4k = 0 \Leftrightarrow k =  - \dfrac{9}{4}\) thì \(\left( * \right) \Leftrightarrow {x^4} = 0 \Leftrightarrow x = 0\) hay \(\left( * \right)\) có nghiệm duy nhất.

+) Nếu \(9 + 4k < 0 \Leftrightarrow k <  - \dfrac{9}{4}\) thì \(\left( * \right)\) vô nghiệm.

Vậy: +) \(k =  - \dfrac{9}{4}\) : (C) và (P) có một điểm chung là \(\left( {0; - \dfrac{9}{4}} \right)\)

+) \(k >  - \dfrac{9}{4}\):  (C) và (P) có hai giao điểm.

+) \(k <  - \dfrac{9}{4}\) : (C) và (P) không cắt nhau.

Cho hàm số: \(y = \dfrac{{2x + 1}}{{x - 2}}\).

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng \( - 5\).

(Đề thi tốt nghiệp THPT năm 2009)

LG câu a

Phương pháp:

- Tìm TXĐ.

- Xét sự biến thiên.

- Vẽ đồ thị hàm số.

Cách giải:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).

Có \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \in D\) nên hàm số nghịch biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).

Giới hạn: \(\mathop {\lim }\limits_{x \to  \pm \infty } y = 2\) nên TCN \(y = 2\).

\(\mathop {\lim }\limits_{x \to {2^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} y =  - \infty \) nên TCĐ \(x = 2\).

Bảng biến thiên:

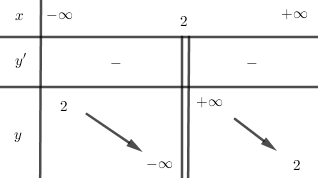
Đồ thị:

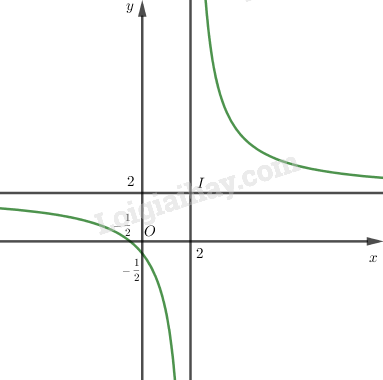
LG câu b

Phương pháp:

- Giải phương trình \(y' = k\) tìm hoành độ giao điểm.

- Viết phương trình tiếp tuyến theo công thức \(y = k\left( {x - {x_0}} \right) + {y_0}\).

Cách giải:

Ta có: \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} =  - 5\)\( \Leftrightarrow {(x - 2)^2} = 1\) \( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)

Với \(x = 3\) ta có \(y = 7\) nên phương trình tiếp tuyến là \(y =  - 5\left( {x - 3} \right) + 7\) hay \(y =  - 5x + 22\).

Với \(x = 1\) ta có \(y =  - 3\) nên phương trình tiếp tuyến là \(y =  - 5\left( {x - 1} \right) - 3\) hay \(y =  - 5x + 2\).

Cho hàm số: \(y = \dfrac{{4 - x}}{{2x + 3m}}\).

a) Xét tính đơn điệu của hàm số.

b) Chứng minh rằng với mọi \(m\), tiệm cận ngang của đồ thị \(\left( {{C_m}} \right)\) của hàm số đã cho luôn đi qua điểm  \(B\left( { - \dfrac{7}{4}; - \dfrac{1}{2}} \right)\).

c) Biện luận theo \(m\) số giao điểm của \(\left( {{C_m}} \right)\) và đường phân giác của góc phần tư thứ nhất.

d) Vẽ đồ thị của hàm số: \(y = \left| {\dfrac{{4 - x}}{{2x + 3}}} \right|\)

LG câu a

Phương pháp:

- Tính \(y'\).

- Biện luận theo \(m\) dấu của \(y'\), từ đó suy ra tính đơn điệu của hàm số.

Cách giải:

TXĐ: \(\mathbb{R}\backslash \left\{ { - \dfrac{{3m}}{2}} \right\}\)

\(y' = \dfrac{{ - 2x - 3m - 2(4 - x)}}{{{{(2x + 3m)}^2}}} = \dfrac{{ - 3m - 8}}{{{{(2x + 3m)}^2}}}\)

+) Nếu \(m <  - \dfrac{8}{3} \Rightarrow y' > 0\) suy ra hàm số đồng biến trên các khoảng  \(\left( { - \infty ; - \dfrac{{3m}}{2}} \right),\left( { - \dfrac{{3m}}{2}; + \infty } \right)\)

+) Nếu \(m >  - \dfrac{8}{3} \Rightarrow y' < 0\) suy ra hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \dfrac{{3m}}{2}} \right),\left( { - \dfrac{{3m}}{2}; + \infty } \right)\)

+) Nếu \(m =  - \dfrac{8}{3}\) thì \(y =  - \dfrac{1}{2}\) khi \(x \ne 4\) là hàm hằng.

LG câu b

Phương pháp:

- Tìm phương trình đường tiệm cận ngang của đồ thị hàm số.

Sử dụng định nghĩa: \(\mathop {\lim }\limits_{x \to  + \infty } y = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to  - \infty } y = {y_0}\) thì \(y = {y_0}\) là TCN của đồ thị hàm số.

Cách giải:

Ta có: \(\mathop {\lim }\limits_{x \to  \pm \infty } \dfrac{{4 - x}}{{2x + 3m}} = \mathop {\lim }\limits_{x \to  \pm \infty } \dfrac{{\dfrac{4}{x} - 1}}{{2 + \dfrac{{3m}}{x}}} =  - \dfrac{1}{2}\)

Nên với mọi \(m\), đường thẳng \(y =  - \dfrac{1}{2}\) là tiệm cận ngang và luôn đi qua \(B\left( { - \dfrac{7}{4}; - \dfrac{1}{2}} \right)\).

LG câu c

Phương pháp:

- Xét phương trình hoành độ giao điểm.

- Biện luận số giao điểm dựa vào số nghiệm của phương trình vừa xét.

Cách giải:

Số giao điểm của \(\left( {{C_m}} \right)\) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình \(\dfrac{{4 - x}}{{2x + 3m}} = x\)

Ta có: \(\dfrac{{4 - x}}{{2x + 3m}} = x\) \( \Leftrightarrow 4 - x = 2{x^2} + 3mx\) với \(x \ne  - \dfrac{{3m}}{2}\)

\( \Leftrightarrow 2{x^2} + (3m + 1)x - 4 = 0\) với \(x \ne  - \dfrac{{3m}}{2}\)

Do \(x \ne  - \dfrac{{3m}}{2}\) nên \(m =  - \dfrac{{3m}}{2}\) không nghiệm đúng phương trình.

Hay \(2.{\left( { - \dfrac{{3m}}{2}} \right)^2} - \dfrac{{9{m^2}}}{2} - \dfrac{{3m}}{2} - 4\)\( = \dfrac{{9{m^2}}}{2} - \dfrac{{9{m^2}}}{2} - \dfrac{{3m}}{2} - 4 \ne 0\) \( \Rightarrow m \ne  - \dfrac{8}{3}\)

Như vậy, để \(x =  - \dfrac{{3m}}{2}\) không là nghiệm của phương trình  (*), ta phải có \(m \ne  - \dfrac{8}{3}\).

Ta có: \(\Delta  = {(3m + 1)^2} + 32 > 0,\forall m\). Từ đó suy ra với \(m \ne  - \dfrac{8}{3}\) đường thẳng \(y = x\) luôn cắt \(\left( {{C_m}} \right)\) tại hai điểm phân biệt.

LG câu d

Phương pháp:

- Vẽ đồ thị hàm số \(y = \dfrac{{4 - x}}{{2x + 3}}\).

- Vẽ đồ thị hàm số \(y = \left| {\dfrac{{4 - x}}{{2x + 3}}} \right|\) bằng cách:

+ Giữ nguyên phần đồ thị phía trên trục \(Ox\).

+ Lấy đối xứng phần dưới qua trục \(Ox\) và xóa phần dưới cũ đi.

Cách giải:

Ta có:  \(y = \left| {\dfrac{{4 - x}}{{2x + 3}}} \right| = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{4 - x}}{{2x + 3}},khi\dfrac{{4 - x}}{{2x + 3}} \ge 0}\\{ - \dfrac{{4 - x}}{{2x + 3}},khi\dfrac{{4 - x}}{{2x + 3}} < 0}\end{array}} \right.\)

Trước hết, ta vẽ đồ thị \(\left( C \right)\) của hàm số \(y = \dfrac{{4 - x}}{{2x + 3}}\).

TXĐ: \(D = R\backslash \left\{ { - \dfrac{3}{2}} \right\}\).

Vì \(y' = \dfrac{{ - 11}}{{{{(2x + 3)}^2}}} < 0\) với mọi \(x \ne  - \dfrac{3}{2}\) nên hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \dfrac{3}{2}} \right);\left( { - \dfrac{3}{2}; + \infty } \right)\).

Bảng biến thiên: 

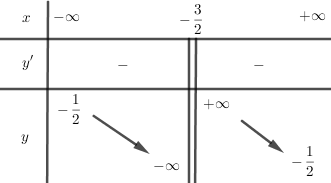
Đồ thị hàm số có đường tiệm cận đứng \(x =  - \dfrac{3}{2}\), tiệm cận ngang \(y =  - \dfrac{1}{2}\).

Đồ thị \(\left( C \right)\) đi qua các điểm \(\left( {0;\dfrac{4}{3}} \right),(4;0)\).

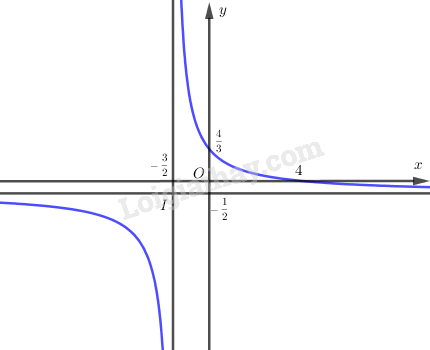
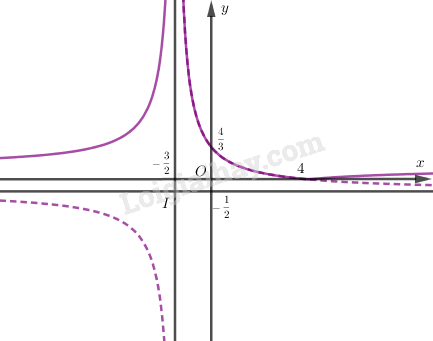
Để vẽ đồ thị \(\left( {C'} \right)\) của hàm số \(y = \left| {\dfrac{{4 - x}}{{2x + 3}}} \right|\), ta giữ nguyên phần đồ thị \(\left( C \right)\) nằm phía trên trục hoành và lấy đối xứng phần đồ thị \(\left( C \right)\) nằm phía dưới trục hoành qua trục hoành.

Hàm số \(y = {x^3} + \left( {m + 3} \right){x^2} + mx - 2\) đạt cực tiểu tại \(x = 1\) khi:

A. \(m = 1\)            B. \(m = 2\)

C. \(m =  - 3\)        D. \(m = 4\)

Hàm số \(y = {x^4} + \left( {{m^2} - 4} \right){x^2} + 5\) có ba cực trị khi:

A. \( - 2 < m < 2\)             B. \(m = 2\)

C. \(m <  - 2\)                    D. \(m > 2\)

Biểu thức tổng quát của hàm số có đồ thị như hình \(1.6\) là:

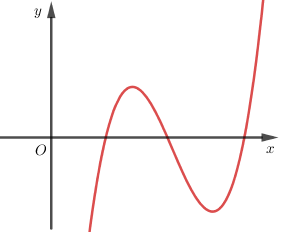
A. \(y = a{x^2} + bx + c\) với \(a \ne 0\).

B. \(y = a{x^3} + cx + d\) với \(a < 0\).

C. \(y = a{x^3} + b{x^2} + cx + d\) với \(a > 0\) và \({b^2} - 3ac > 0\).

D. \(y = {x^3}\).

Xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3\left( {m - 1} \right){x^2} - 3\left( {m + 1} \right)x - 5\) có cực trị.

A. \(m > 0\)                          B. \( - 1 < m < 1\)

C. \(m \le 0\)                         D. \(\forall m \in \mathbb{R}\)

Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4}-2{x^2}\) tại điểm có hoành độ \(x =  - 2\) là:

A. \(y =  - 24x + 40\)        B. \(y = 24x - 40\)

C. \(y =  - 24x - 40\)         D. \(y =  - 24x\)

Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với đường thẳng \(y = 24x - 1\) là:

A. \(y = 24x - 43\)                B. \(y =  - 24x - 43\)

C. \(y = 24x + 43\)                D. \(y = 24x + 1\)

Giao điểm của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{2x - 1}}\) với đường thẳng \(y = x + 2\) là:

A. \(\left( {1;3} \right)\) và \(\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right)\)

B. \(\left( {1;3} \right)\) và \(\left( {0;2} \right)\)

C. \(\left( {0; - 1} \right)\) và \(\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right)\)

D. \(\left( {0; - 1} \right)\) và \(\left( {0;2} \right)\)