a) \(y = \dfrac{x}{{4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\)
Ta có: \(y' = \dfrac{{4 - {x^2}}}{{{{(4 + {x^2})}^2}}};\)\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Bảng biến thiên:
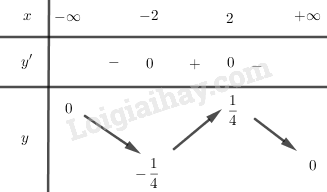
Từ đó ta có \(\mathop {\min }\limits_R f(x) = - \dfrac{1}{4};\mathop {\max }\limits_R f(x) = \dfrac{1}{4}\)
b) \(y = \dfrac{1}{{\cos x}}\) trên khoảng \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\)
Ta có: \(y' = \dfrac{{\sin x}}{{{{\cos }^2}x}};\)\(y' = 0 \Rightarrow x = \pi \in \left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\)
Bảng biến thiên:
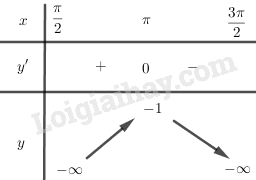
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: \(\mathop {\max }\limits_{\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)} y = y(\pi ) = - 1\)