Ta có: \({x^3}-3{x^2}-m = 0\)\( \Leftrightarrow m = {x^3} - 3{x^2}\)
Xét hàm \(f\left( x \right) = {x^3} - 3{x^2}\) có \(f'(x) = 3{x^2} - 6x\)\( = 3x(x - 2) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\).
Bảng biến thiên:
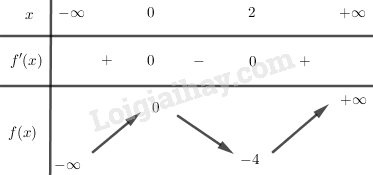
Phương trình \({x^3}-3{x^2}-m = 0\) có ba nghiệm phân biệt khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm phân biệt.
Từ bảng biến thiên suy ra \( - 4 < m < 0\) thỏa mãn bài toán.