Xét hai trường hợp:
a) \(M\) ở bên trong đường tròn (hình a)
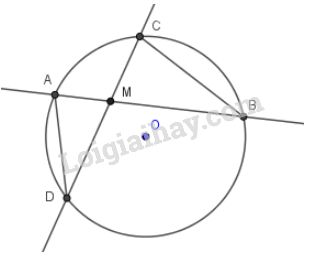
Xét hai tam giác \(MAD\) và \(MCB\) có:
\(\widehat{AMD}\) = \(\widehat{CMB}\) ( đối đỉnh)
\(\widehat{ADM}\) = \(\widehat{CBM}\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Do đó \(∆MAD\) đồng dạng \(∆MCB\) (g-g), suy ra:
\(\dfrac{MA}{MC}=\dfrac{MD}{MB}\), do đó \(MA. MB = MC. MD\)
b) M ở bên ngoài đường tròn (hình b)
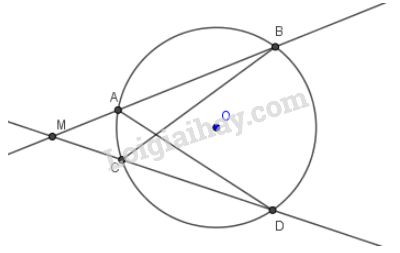
Tương tự, xét hai tam giác \(MAD\) và \(MCB\) có:
\(\widehat{M}\) chung
\(\widehat{MDA}\) = \(\widehat{MBC}\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Nên \(∆MAD\) đồng dạng \(∆MCB\) (g-g)
Suy ra: \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\)
hay \(MA. MB = MC. MD\)