Bài 7. Tứ giác nội tiếp
Bài Tập và lời giải
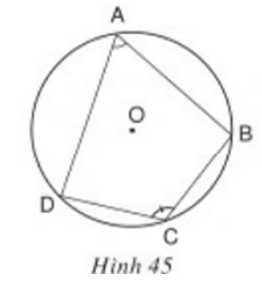
a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.
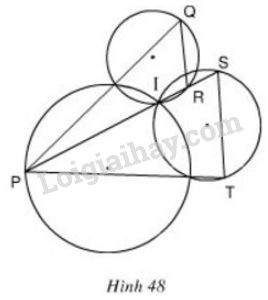
b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba đỉnh nằm trên đường tròn đó còn đỉnh thức tư thì không.
Tứ giác \(ABCD\) có \(\widehat{ABC}+ \widehat{ADC}= 180^0\). Chứng minh rằng các đường trung trực của \(AC,\, BD, \,AB\) cùng đi qua một điểm.
Cho \(ABCD\) là một tứ giác nội tiếp đường tròn tâm \(M,\) biết \(\widehat {DAB}= 80^0\), \(\widehat {DAM}= 30^0,\) \(\widehat {BMC}= 70^0\).
Hãy tính số đo các góc \(\widehat {MAB},\) \(\widehat {BCM},\) \(\widehat {AMB},\) \(\widehat {DMC},\) \(\widehat {AMD},\) \(\widehat {MCD}\) và \(\widehat {BCD}.\)
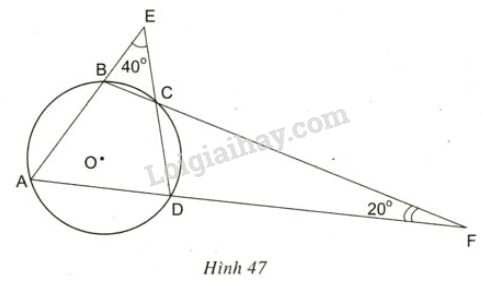
Xem hình 47. Hãy tìm số đo các góc của tứ giác \(ABCD.\)
Trong các hình sau, hình nào nội tiếp được một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân ? Vì sao?
Cho tam giác đều \(ABC.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A,\) lấy điểm \(D\) sao cho \(DB = DC\) và \(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.\)
a) Chứng minh \(ABDC\) là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm \(A,\, B,\, D, \,C\).
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)
Cho đường tròn (O) đường kính AB. Từ A kẻ hai đường thẳng cắt đường tròn tại C và D, cắt tiếp tuyến của đường tròn vẽ qua B tại E và F.
a) Chứng minh các điểm C, E, F, D cùng thuộc một đường tròn.
b) Chứng minh: \(FB^2= FA.FD\).
Cho tam giác ABC nội tiếp trong đường tròn (O), xy là tiếp tuyến tại A của đường tròn. Một đường thẳng song song với xy cắt AB, AC lần lượt tại D và E. Chứng minh tứ giác BDEC nội tiếp.
Tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O). Đường tròn đường kính BC cắt AB, AC lần lượt tại E và F. BF, CE cắt nhau tại H.
a) Chứng minh H là trực tâm của tam giác ABC.
b) Gọi K là điểm đối xứng với H qua BC. Chứng minh tứ giác ABKC nội tiếp.
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác trong của hai góc B và C và J là giao điểm các phân giác ngoài của hai góc đó.
a) Chứng minh BICJ là tứ giác nội tiếp.
b) Chứng minh rằng ba điểm A, I, J thẳng hàng.
Từ điểm M ở ngoài đường tròn (O), kẻ cát tuyến MAB ( A nằm giữa hai điểm M và B) và các tiếp tuyến MC, MD. Gọi H là giao điểm của OM và CD.
a) Chứng minh : MC2 = MA.MB.
b) Chứng minh tứ giác AHOB nội tiếp.
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là điểm tùy ý trên đường thẳng AB, nằm ngoài đoạn AB. Vẽ qua M hai cát tuyến MCD và MC’D’ với (O) và (O’). Chứng minh tứ giác CDD’C’ nội tiếp.
Cho góc \(\widehat {xAy}\) và đường tròn (O tiếp xúc với Ax và Ay tại B và C. Trên đoạn thẳng BC lấy điểm M ( khác B và C). Đường thẳng vuông góc với OM tại M cắt Ax, Ay lần lượt tại D và E. Chứng minh các điểm A, D, O, E cùng nằm trên một đường tròn.
Trên các cạnh BC và CD của hình vuông ABCD lấy các điểm E và F sao cho
\(\widehat {EAF} = 45^\circ \) . Các đoạn thẳng AE, AF cắt BD theo thứ tự ở H và K. Chứng minh tứ giác EHKF nội tiếp.
M là một điểm thuộc cung nhỏ BC. Tiếp tuyến tại M cắt AB, AC lần lượt ở D và E. Gọi I và K lần lượt là giao điểm của OD, OE với BC. Chứng minh rằng tứ giác OBDK nội tiếp.
Cho tam giác ABC nội tiếp trong đường tròn (O). Từ một điểm bất kì trên đường tròn hạ các đường vuông góc xuống các cạnh. Chứng minh rằng chân ba đường vuông góc này thẳng hàng (đường thẳng Sim-Sơn).