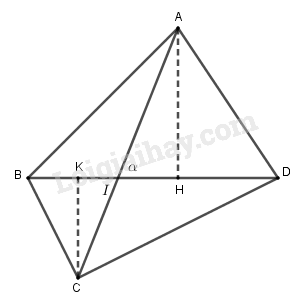
a) Ta có: \({S_{ABCD}} = {S_{ABD}} + {S_{CBD}}\)
Vẽ AH và CK vuông góc với BD.
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: \(AH = AI\sin \alpha \), \(AK = CI\sin \alpha \)
\({S_{ABCD}} = \dfrac{1}{2}AH.BD + \dfrac{1}{2}CK.BD\)
\( = \dfrac{1}{2}BD\left( {AH + CK} \right)\)
\( = \dfrac{1}{2}BD\left( {AI + IC} \right)sin\alpha \)\( = \dfrac{1}{2}BD.AC\sin \alpha \)
Vậy \({S_{ABCD}} = \dfrac{1}{2}x.y\sin \alpha \).
b) Nếu \(AC \bot BD\) thì \(\sin \alpha = 1\), khi đó \({S_{ABCD}} = \dfrac{1}{2}x.y\).
Như vậy nếu tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau thì diện tích của tứ giác bằng một nửa tích độ dài của hai đường chéo.