a)
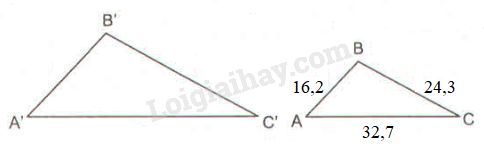
Vì \(∆ A’B’C’\) đồng dạng \(∆ ABC \) nên ta có:
\(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}}\)
Mà \(AB = 16,2cm; BC = 24,3 cm;\)\(\; AC = 32,7 cm\) nên \(A'B' = AB + 10,8 = 16,2 + 10,8 \)\(\,= 27 \;(cm)\)
Ta có \(\displaystyle {{27} \over {16,2}} = {{A'C'} \over {32,7}} = {{B'C'} \over {24,3}}\)
\( \Rightarrow \displaystyle A'C' = {{27.32,7} \over {16,2}} = 54,5\; (cm)\).
\( \Rightarrow \displaystyle B'C' = {{27.24,3} \over {16,2}} = 40,5\; (cm)\).
b)
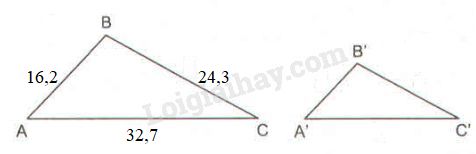
Vì \( ∆ A’B’C’\) đồng dạng \(∆ ABC \) nên ta có \(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}}\)
Mà \( AB = 16,2cm; BC = 24,3 cm;\)\(\; AC = 32,7 cm\) nên \(A'B' = AB - 5,4 = 16,2 - 5,4 \)\(\,= 10,8\; (cm)\)
Ta có: \(\displaystyle {{10,8} \over {16,2}} = {{A'C'} \over {32,7}} = {{B'C'} \over {24,3}}\)
\( \Rightarrow \displaystyle A'C' = \dfrac{{10,8.32,7}}{{16,2}} = 21,8\; (cm)\).
\( \Rightarrow \displaystyle B'C' = \dfrac{{10,8.24,3}}{{16,2}} = 16,2\; (cm)\).