a) Hình a
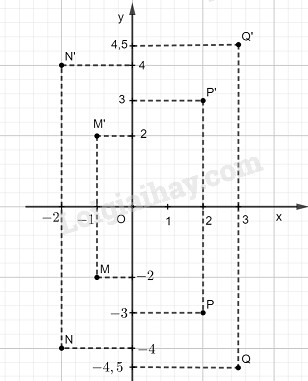
Tọa độ các điểm \(M’, N’, P’ , Q’\) lần lượt đối xứng với các điểm \(M , N, P, Q\) qua trục \(Ox\):
\(M'\left( {1 - ;2} \right),N'\left( { - 2;4} \right),\)\(P'\left( {2;3} \right),Q'\left( {3;4,5} \right)\)
b) Hình b
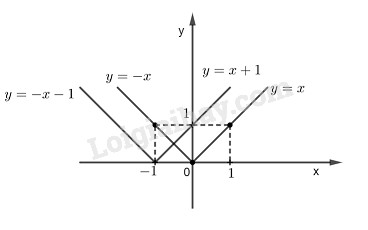
*Ta có:
\(y = \left| x \right| = \left\{ \matrix{
x\,\,\,\,\,\,\,\,nếu\,\,\,x \ge 0 \hfill \cr
- x\,\,\,\,\,\,\,nếu\,\,\,x \le 0 \hfill \cr} \right.\)
Đồ thị hàm số \(y = x\) đi qua gốc tọa độ O và điểm \((1;1)\)
Đồ thị hàm số \(y = -x\) đi qua gốc tọa độ O và điểm \((-1;1)\)
* Ta có :\(y = \left| {x + 1} \right| \)\(= \left\{ \matrix{x + 1\,\,\,\,\,\,nếu\,\,\,x \ge - 1 \hfill \cr
- \left( {x + 1} \right)\,nếu\,\,\,x \le - 1 \hfill \cr} \right.\)
- Vẽ đồ thị hàm số \(y = x + 1\)
Cho \(x = 0\) thì \(y = 1.\) Ta có: \((0;1)\)
Cho \(y = 0\) thì \(x = -1.\) Ta có: \((-1;0)\)
Đồ thị hàm số \(y = x + 1\) đi qua hai điểm \((0;1)\) và \((-1;0)\)
- Vẽ đồ thị hàm số \(y = - (x + 1)\)
Cho \(x = 0\) thì \(y = -1.\) Ta có : \((0;-1)\)
Cho \(y = 0\) thì \(x = -1.\) Ta có : \((-1;0)\)
Đồ thị hàm số \(y = - (x + 1)\) đi qua hai điểm \((0;-1)\) và \((-1;0)\)
c) Ta có : \(y = x\) và \(y = x + 1\) song song với nhau
\(y = -x\) và \(y = -(x + 1)\) song song với nhau
Suy ra chỉ có đồ thị hàm số \(y = -x\) và \(y = x + 1\) cắt nhau
Phương trình hoành độ giao điểm:
\( - x = x + 1 \Leftrightarrow 2x = - 1 \Leftrightarrow x = - \dfrac{1}{2}\)
Suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất.
Tung độ giao điểm: \(y = - x \Rightarrow y = \dfrac{1}{2}\)
Vậy tọa độ giao điểm của đường thẳng \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\) là : \(I\left( { - \dfrac{1}{2};\dfrac{1 }{2}} \right)\)