Thực hiện phép tính sau:
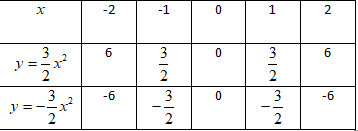
+) Đối với hàm số \(y=\dfrac{3}{2}x^2\):
\(x=-2 \Rightarrow y=\dfrac{3}{2}.(-2)^2=\dfrac{3}{2}.4=6\).
\(x=-1 \Rightarrow y=\dfrac{3}{2}.(-1)^2=\dfrac{3}{2}.1=\dfrac{3}{2}\).
\(x=0 \Rightarrow y=\dfrac{3}{2}.0=0\).
\(x=1 \Rightarrow y=\dfrac{3}{2}.1^2=\dfrac{3}{2}\).
\(x=2 \Rightarrow y=\dfrac{3}{2}.2^2=\dfrac{3}{2}.4=6\)
+) Đối với hàm số \(y=-\dfrac{3}{2}x^2\):
\(x=-2 \Rightarrow y=-\dfrac{3}{2}.(-2)^2=-\dfrac{3}{2}.4=-6\).
\(x=-1 \Rightarrow y=-\dfrac{3}{2}.(-1)^2=-\dfrac{3}{2}.1=-\dfrac{3}{2}\).
\(x=0 \Rightarrow y=-\dfrac{3}{2}.0=0\).
\(x=1 \Rightarrow y=-\dfrac{3}{2}.1^2=-\dfrac{3}{2}\).
\(x=2 \Rightarrow y=-\dfrac{3}{2}.2^2=-\dfrac{3}{2}.4=-6\)
Ta được bảng sau:
Vẽ đồ thị:
+) Vẽ đồ thị hàm số \(y=\dfrac{3}{2}x^2\)
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
\(A(-2; 6);\ B{\left(-1; \dfrac{3}{2}\right)};\ O(0; 0);\ C{\left(1; \dfrac{3}{2}\right)};\ D(2; 6)\)
+) Vẽ đồ thị hàm số \(y=-\dfrac{3}{2}x^2\)
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
\(A'(-2; -6);\ B'{\left(-1; -\dfrac{3}{2}\right)};\ O(0; 0);\)
\(\ C'{\left(1; -\dfrac{3}{2}\right)};\ D'(2; -6)\)
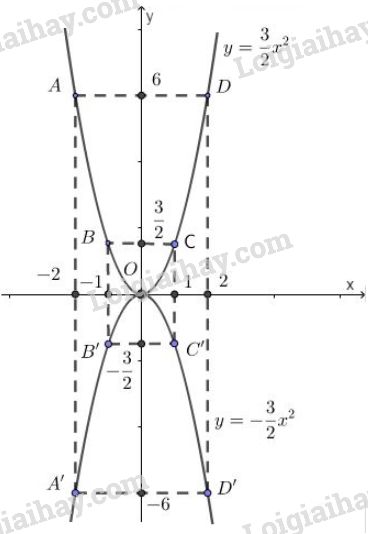
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục \(Ox\).