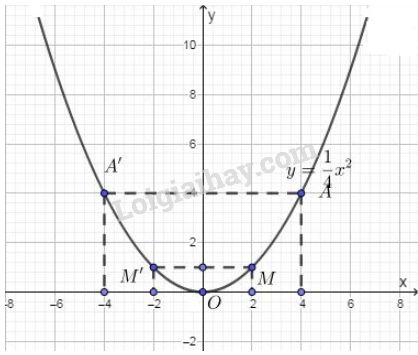
a) Vì \(M(2;1)\) thuộc hàm số \(y=ax^2\), thay \(x=2,\ y=1\) vào công thức hàm số, ta có:
\(1=a.2^2 \Leftrightarrow 1=a.4 \Leftrightarrow a=\dfrac{1}{4}\)
Khi đó , hàm số đã cho có dạng là: \(y=\dfrac{1}{4}x^2\) (1).
b) Thay \(x=4,\ y=4\) vào công thức hàm số (1), ta được:
\(4=\dfrac{1}{4}.4^2 \) \(\Leftrightarrow 4=\dfrac{16}{4}\) (luôn đúng)
Vậy điểm \(A(4; 4)\) thuộc đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\).
c) Ta có điểm \(A'(-4;4)\) cũng đối xứng với điểm \(A(4; 4)\).
Điểm \(M'(-2; 1)\) đối xứng với điểm \(M(2; 1)\).
Vì đồ thị hàm số \(y=\dfrac{1}{2}x^2\) là đường cong đi qua gốc tọa độ, nhận trục \(Oy\) làm trục đối xứng nên \(A',\ M'\) cũng thuộc đồ thị.