a) \(y = {{ - x + 2} \over {x + 2}}\)
+) Tập xác định: D = R\{-2}
+) Ta có: \(y' = - {4 \over {{{(x + 2)}^2}}}\)
Bảng biến thiên:
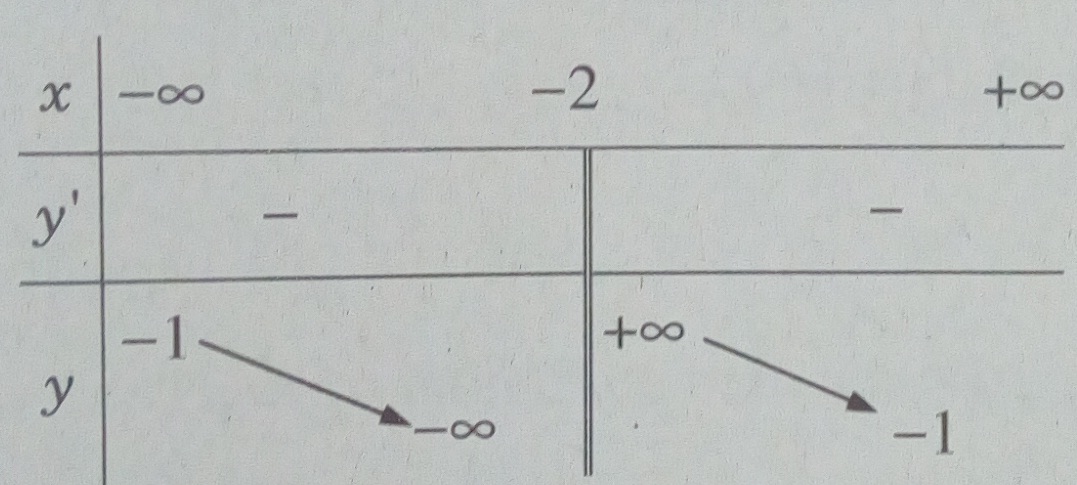
Hàm số nghịch biến trên các khoảng \(( - \infty ; - 2),( - 2; + \infty )\)
+) Tiệm cận đứng x = -2 vì \(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty \)
Tiệm cận ngang y = -1 vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = - 1\)
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
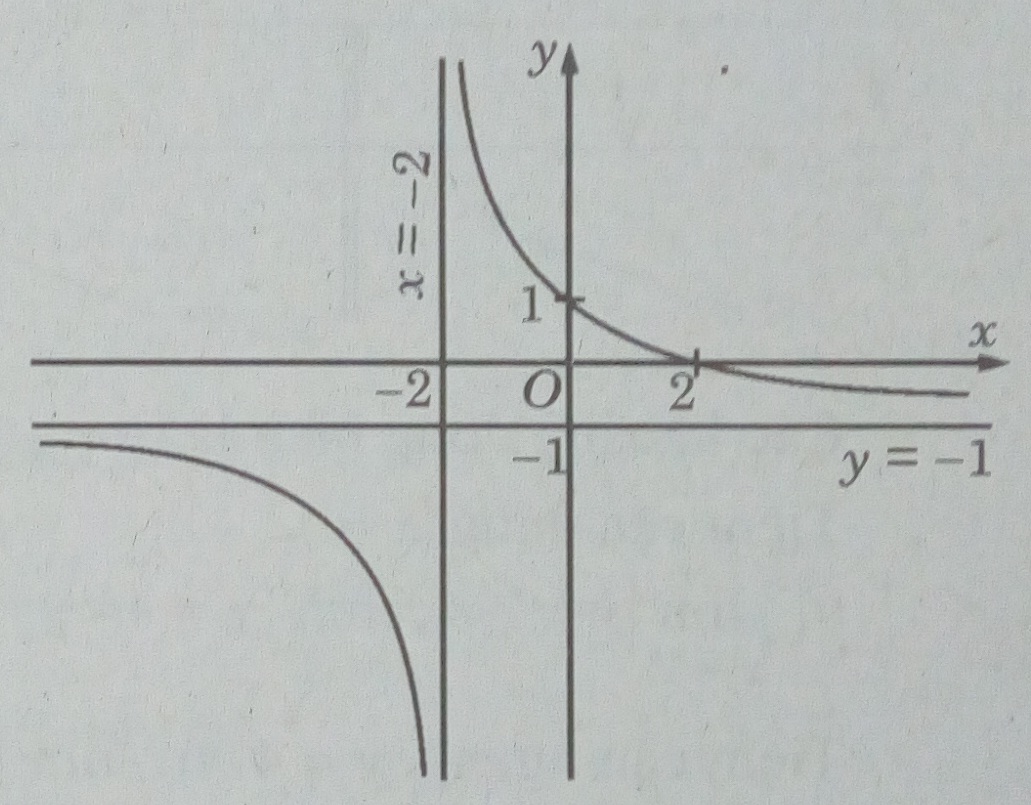
b) Tiếp tuyến của đồ thị có hệ số góc k = -4 (vì vuông góc với đường thẳng \(y = {1 \over 4}x - 42\) )
Hoành độ tiếp điểm thỏa mãn phương trình:
\({{ - 4} \over {{{(x + 2)}^2}}} = - 4 = > \left[ {\matrix{{{x_1} = - 3} \cr {{x_2} = - 1} \cr} } \right.\)
Ứng với \({x_1} = - 3\) ,ta có tiếp tuyến y = - 4x – 17
Ứng với \({x_2} = - 1\), ta có tiếp tuyến y = - 4x – 1.