Gọi \(y\) (km) là quãng đường đi được và \(x\) (h) là thời gian đi trên quãng đường.
Theo đề bài \(y=140\,km\) và vận tốc \(v=35\;km/h\).
Ta biết quãng đường \(y\) và thời gian \(x\) là hai đại lượng tỉ lệ thuận nên ta có:
\(y=35x\) (1)
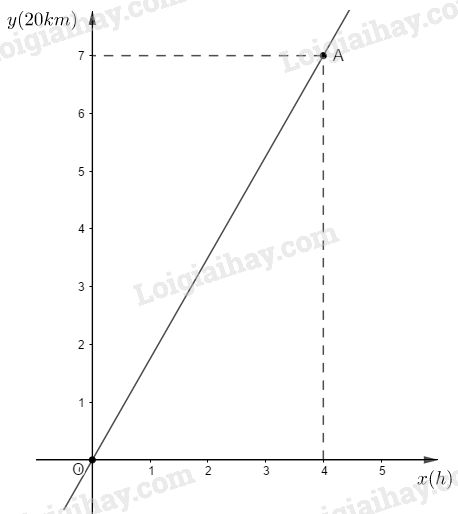
Mặt khác một đơn vị trên trục hoành \(Ox\) biểu thị \(1\) giờ và một đơn vị trên trục tung biểu thị \(20\,km\) nên hệ trục tọa độ \(Oxy\) và đồ thị của chuyển động được vẽ như sau:
Công thức (1) biểu diễn hàm số dạng \(y=ax\) nên đồ thị của chuyển động là đường thẳng đi qua gốc tọa độ. Ta cần xác định điểm thứ hai:
Từ (1) suy ra \(x = \dfrac{y}{{35}}\). Vậy khi \(y=140\) thì \(x= \dfrac{{140}}{{35}} = 4\) ta có tọa độ \((4;140)\) xác định điểm \(A\) thuộc đồ thị của hàm số \(y=35x\).
Vẽ đường thẳng qua \(O(0;0)\) và \(A(4;140)\) được đồ thị của chuyển động (hình vẽ).