Bài 1: Gọi x, y, z là số tờ tiền của loại tiền mệnh giá 2000 đồng và 5000 đồng và 10 000 đồng ; \(x,y,z \in {\mathbb N^*}\)
Vì tổng giá trị của mỗi loại bằng nhau nên ta có :
\(\eqalign{ & 2000x = 5000y = 10000z \cr & \Rightarrow {{2000x} \over {10000}} = {{5000y} \over {10000}} = {{10000z} \over {10000}} \cr} \)
\( \Rightarrow {x \over 5} = {y \over 2} = {z \over 1} = {{x + y + z} \over {5 + 2 + 1}}\) , trong đó : \(x + y + z = 16\)
Vậy \({x \over 5} = {y \over 2} = {z \over 1} = {{16} \over 8} = 2\)
\(\Rightarrow x = 5.2 = 10;y = 2.2 = 4;\)\(\;z = 1.2 = 2\)
Vậy loại tiền 2000 đồng có 10 tờ, 5000 đồng có 4 tờ ; 10 000 đồng có 2 tờ.
Bài 2: Đồ thị của hàm số \(y = -2x\) có đường thẳng qua gốc tọa độ O và điểm \(P(1 ;-2)\)
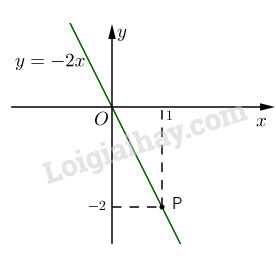
Thế tọa độ của điểm \(M(-5 ;10)\) vào công thức \(y = -2x \); với \(x = -5 ; y = 10.\)
Ta có : \(10 = (-2).(-5)\) hay \(10 = 10\) (luôn đúng).
Vậy M thuộc đồ thị hàm số \(y = -2x.\)
Tương tự như M, ta thấy A,B thuộc đồ thị hàm số \(y = -2x\) (là đường thẳng) Vậy O, A, B thẳng hàng.
Bài 3: Trong tam giác ABC, ta có \(\widehat A + \widehat B + \widehat C = {180^0}.\)
Vì \(\widehat A,\widehat B,\widehat C\) tỉ lệ thuận với \({1 \over 2};{1 \over 3};{1 \over 6}\) .
\({{\widehat A} \over {{1 \over 2}}} = {{\widehat B} \over {{1 \over 3}}} = {{\widehat C} \over {{1 \over 6}}} = {{\widehat A + \widehat B + \widehat C} \over {{1 \over 2} + {1 \over 3} + {1 \over 6}}} = {{{{180}^0}} \over 1}\)
\( \Rightarrow \widehat A = {{{{180}^0}} \over 2} = {90^0};\widehat B = {{{{180}^0}} \over 3} = {60^0};\)\(\;\widehat C = {{{{180}^0}} \over 6} = {30^0}\)
Vậy \(\widehat A = {90^0};\widehat B = {60^0};\widehat C = {30^0}.\)
Bài 4:
\(f\left( {{1 \over 2}} \right) = 2 \Rightarrow 2 = m.\left( {{1 \over 2}} \right) \Rightarrow m = - 4.\)