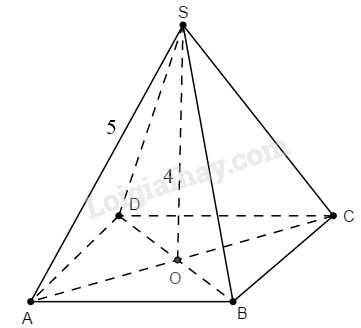
Giả sử hình chóp tứ giác đều \(S.ABCD\) có độ dài cạnh bên là \(5cm\), chiều cao \(4cm.\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SOA\), ta có:
\(S{A^2} = S{O^2} + O{A^2}\)
\(\Rightarrow OA = \sqrt {S{A^2} - S{O^2}} \)
\( \Rightarrow OA = \sqrt {{5^2} - {4^2}} = 3\,\left( {cm} \right)\)
\( \Rightarrow AC=BD =2OA=2.3= 6\;(cm)\).
Diện tích đáy \(ABCD\) là: \(S= \displaystyle{1 \over 2}.6.6 = 18\;(c{m^2})\)
Thể tích hình chóp đều \(S.ABCD\) là:
\(\displaystyle V = \displaystyle {1 \over 3}S.h = {1 \over 3}.18.4 = 24\;(c{m^3})\)
Chọn B.