a) Vì \(AO\) là đường cao hình chóp nên \(∆ AOM \) vuông tại \(O.\)
Ta có: \(\displaystyle OM = {1 \over 2}CD={1 \over 2}.6 = 3\;(cm)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AOM\), ta có:
\( A{M^2} = A{O^2} + O{M^2} = {8^2} + {3^2} = 73\)
\( \Rightarrow AM = \sqrt {73} \;(cm)\)
Ta có: \({S_{xq}} = pd = 6.2.\sqrt {73} = 12\sqrt {73} \;(c{m^2})\).
Diện tích đáy \(BCDE\) là \(S_đ= 6.6 =36 \;(cm^2)\).
Diện tích toàn phần của hình chóp là:
\({S_{TP}} = {S_{xq}} + {S_đ}\)\(\,= 12\sqrt {73} + 36 \approx 138,5\;(c{m^2})\)
b) Hình chóp tứ giác đều, cạnh đáy bằng \(6cm\), chiều cao hình chóp bằng \(5cm.\)
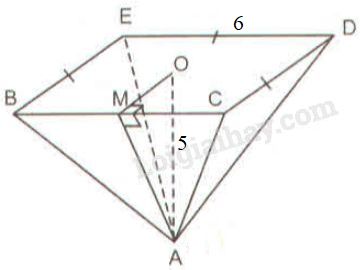
Tương tự hình vẽ câu a ta có \(MA ⊥ BC.\)
Ta có \(\displaystyle OM = {1 \over 2}CD={1 \over 2}.6 = 3\;(cm)\)
Vì \(AO\) là đường cao của hình chóp nên \(∆ AOM\) vuông tại \(O.\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AOM,\) ta có:
\( A{M^2} = O{A^2} + O{M^2} \)\(\,= 5^2 + 3^2 = 34 \)
\( \Rightarrow AM = \sqrt {34}\;(cm). \)
Diện tích xung quanh hình chóp là:
\(S_{xq}=6.2.\sqrt {34} = 12\sqrt {34} (c{m^2})\)
Diện tích đáy \(BCDE\) là \(S_đ= 6.6 =36 \;(cm^2)\).
Diện tích toàn phần của hình chóp là:
\({S_{TP}} = {S_{xq}} + {S_đ}\)\(\,=12\sqrt {34} + 36 \approx 106\,(c{m^2})\)
c) Hình chóp tứ giác đều, cạnh đáy bằng \(20cm,\) chiều cao hình chóp bằng \(7cm.\)
Tương tự hình vẽ câu a ta có: \(MA ⊥ BC\)
Ta có \(\displaystyle OM = {1 \over 2}CD={1 \over 2}.20 = 10\;(cm)\)
Vì \(AO \) là đường cao của hình chóp nên \(∆ AOM\) vuông tại \(O.\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AOM,\) ta có:
\( A{M^2} = O{A^2} + O{M^2} \)\(\,= 7^2 + 10^2 = 149 \)
\( \Rightarrow AM = \sqrt {149}\;(cm). \)
Diện tích xung quanh hình chóp là:
\(S_{xq}=20.2.\sqrt {149} = 40\sqrt {149} (c{m^2})\)
Diện tích đáy \(BCDE\) là \(S_đ= 20.20 =400 \;(cm^2)\).
Diện tích toàn phần của hình chóp là:
\({S_{TP}} = {S_{xq}} + {S_đ}\)\(\,=40\sqrt {149} + 400 \approx 888,3\,(c{m^2})\)
d) Hình chóp tứ giác đều, cạnh đáy bằng \(1m\), chiều cao hình chóp bằng \(0,5m.\)
Tương tự hình vẽ câu a ta có \(MA ⊥ BC.\)
Ta có \(\displaystyle OM = {1 \over 2}CD={1 \over 2}.1 = 0,5\;(m)\)
Vì \(AO\) là đường cao của hình chóp nên \(∆ AOM\) vuông tại \(O.\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AOM,\) ta có:
\( A{M^2} = O{A^2} + O{M^2} \)\(\,= 0,5^2 + 0,5^2 = 0,5 \)
\( \Rightarrow AM = \sqrt {0,5}\;(m). \)
Diện tích xung quanh hình chóp là:
\(S_{xq}=1.2.\sqrt {0,5} = 2\sqrt {0,5} ({m^2})\)
Diện tích đáy \(BCDE\) là \(S_đ= 1.1 =1 \;(m^2)\).
Diện tích toàn phần của hình chóp là:
\({S_{TP}} = {S_{xq}} + {S_đ}\)\(\,=2\sqrt {0,5} + 1 \approx 2,4\,({m^2})\)