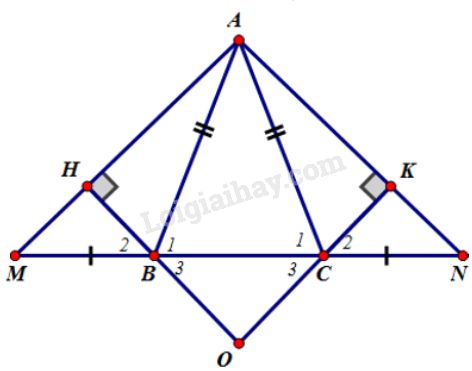
a) \(∆ABC\) cân tại \(A\), suy ra \(\widehat {{B_1}} = \widehat {{C_1}}\) (1)
\(\widehat {{B_1}} + \widehat {ABM} = {180^0}\) (hai góc kề bù) (2)
\(\widehat {{C_1}} + \widehat {ACN} = {180^0}\) (hai góc kề bù) (3)
Từ (1), (2), (3) \(\Rightarrow \widehat {ABM} = \widehat {ACN}\)
Xét \(∆ABM \) và \(∆ACN \) có:
\(AB = AC\) (\(∆ABC\) cân tại \(A\))
\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)
\(BM = CN\) (gt)
\( \Rightarrow ∆ABM = ∆ACN\) (c.g.c)
\(\Rightarrow \widehat M = \widehat N\) (hai góc tương ứng)
Vậy \(∆AMN\) là tam giác cân tại \(A.\)
b) Xét hai tam giác vuông \(BHM\) và \(CKN\) có :
\(BM = CN\) (gt)
\(\widehat M = \widehat N\) (chứng minh trên)
\( \Rightarrow ∆BHM = ∆CKN\) (cạnh huyền - góc nhọn)
\(\Rightarrow BH = CK\) (hai cạnh tương ứng)
c) Theo câu a) ta có tam giác \(AMN\) cân ở \(A\) nên \(AM = AN\) (*)
Theo câu b ta có \(∆BHM = ∆CKN\) nên suy ra \(HM = KN\) (2*).
Từ (*) và (2*) ta có: \(AH = AM – HM = AN – KN = AK\)
Vậy \(AH = AK.\)
d) \(∆BHM = ∆CKN\) suy ra \(\widehat {{B_2}} = \widehat {{C_2}}\) (hai góc tương ứng)
Mà \(\widehat {{B_2}} = \widehat {{B_3}}\) (2 góc đối đỉnh); \(\widehat {{C_2}} = \widehat {{C_3}}\) (2 góc đối đỉnh)
Nên \(\widehat {{B_3}} = \widehat {{C_3}}\) .
Vậy \(∆OBC\) là tam giác cân tại \(O.\)
e) Khi \(\widehat {BAC} = {60^o}\) và \(BM = CN = BC\) hình được vẽ lại như sau:
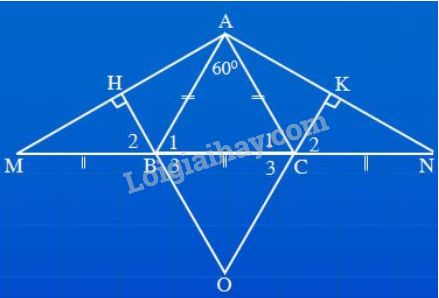
+ Tam giác \(ABC\) cân tại \(A\) có \(\widehat {BAC} = {60^o}\) nên là tam giác đều hay \(AB = BC = AC\).
Mặt khác: \(BM = CN = BC\) (gt)
Do đó: \(AB = BC = AC = BM = CN\).
Ta có: \(\widehat {ABM} = \widehat {ACN} = {120^o}\) (cùng bù với góc \({60^o}\))
Vì \(AB = BM\) (chứng minh trên) nên \(∆ABM\) cân tại \(B\) suy ra \(\widehat M = \widehat {BAM} = \dfrac{{{{180}^o} - {{120}^o}}}{2}= {30^o}\) .
Suy ra \(\widehat {ANM} = \widehat {AMN} = {30^o}\) .
Và \(\widehat {MAN} = {180^o} - \left( {\widehat {AMN} + \widehat {ANM}} \right)\)
\( = {180^o} - {2.30^o} = {120^o}\)
Vậy \(∆AMN\) có \(\widehat M = \widehat N = {30^o};\widehat A = {120^o}.\)
+ \(∆BHM\) vuông tại \(H\) có: \(\widehat M = {30^o}\) nên \(\widehat {{B_2}} = {60^o}\) (trong tam giác vuông hai góc nhọn phụ nhau)
Suy ra \(\widehat {{B_3}}=\widehat {{B_2}} = {60^o}\) (2 góc đối đỉnh)
Tam giác \(OBC\) cân có \(\widehat {{B_3}} = {60^o}\) nên tam giác \(OBC\) là tam giác đều.