Đặt tên các điểm như hình vẽ:
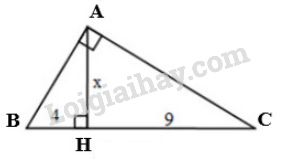
Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:
\(AH^2=BH.CH \)
\(\Leftrightarrow x^2=4.9=36\)
\(\Leftrightarrow x=\sqrt{36}=6\)
Vậy \(x=6\)
b) Đặt tên các điểm như hình vẽ
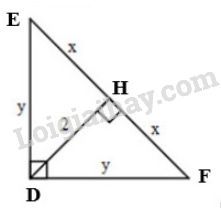
Xét \(\Delta{DEF}\) vuông tại \(D\), đường cao \(DH\). Áp dụng hệ thức \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\), ta được:
\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\) \(\Leftrightarrow \dfrac{1}{2^2}=\dfrac{1}{y^2}+\dfrac{1}{y^2}\)
\(\Leftrightarrow \dfrac{1}{4}=\dfrac{2}{y^2}\)
\(\Leftrightarrow y^2=4.2=8\)
\(\Leftrightarrow y=\sqrt 8=2\sqrt 2\).
Xét \(\Delta{DHF}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:
\(DF^2=DH^2+HF^2 \Leftrightarrow (2\sqrt 2)^2=2^2+x^2\)
\(\Leftrightarrow 8=4+x^2\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow x=\sqrt 4=2\)
Vậy \(x= 2,\ y=2\sqrt 2\).
c) Đặt tên các điểm như hình vẽ:
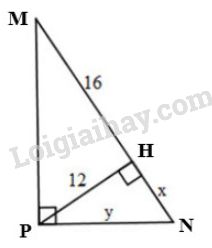
Xét \(\Delta{MNP}\) vuông tại \(P\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:
\(PH^2=HM.HN \Leftrightarrow 12^2=16.x\)
\(\Leftrightarrow 144=16.x\)
\(\Leftrightarrow x=\dfrac{144}{16}=9\)
Xét \(\Delta{PHN}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:
\(PN^2=PH^2+HN^2 \Leftrightarrow y^2=12^2+9^2\)
\(\Leftrightarrow y^2=144+81=225\)
\(\Leftrightarrow y= \sqrt{225}=15\)
Vậy \(x=9,\ y=15\).