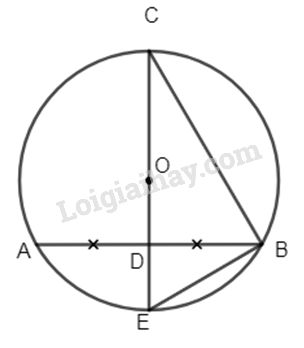
Ta có \(\widehat {CBE} = 90^\circ \) (chắn nửa đường tròn )
D là trung điểm của AB
\(\Rightarrow \) OD vuông góc AB (định lí đường kính dây cung)
Tam giác vuông CBE có đường cao BD nên
\(B{D^2} = CD.DE\)
\( \Rightarrow {3^2} = 9.DE \Rightarrow {\text{ }}DE = 1\left( {cm} \right).\)
Do đó :
\(CE = CD + DE = 9 + 1 = 10\; (cm)\)
Độ dài đường tròn: \(π.CE = 10π.\)